Responde Aí
Acesse com GoogleAcesse com AppleAcesse com Facebook

Exercícios Resolvidos de Reflexão Ortogonal

Ver Teoria
Exercício 9123456781011121314151617

Enunciado

UFRJ, Álgebra Linear, P4 – 2017.1, Questão 11

Considere um vetor v → de R 2 e r , a reta de equação a x + b y = 0 :

I   - A projeção ortogonal de v → em r é igual à projeção ortogonal de v → na direção do vetor ( a ,   b )

I I   - A reflexão ortogonal de v → por r é igual à menos a projeção ortogonal de v → na direção do vetor ( - b ,   a )

(a) Ambas são falsas

(b)   I é falsa e I I é verdadeira

(c) Ambas são verdadeiras

(d) I é verdadeira e I I é falsa

Passo 1

Primeiro vamos achar o vetor diretor dessa reta r :

a x + b y = 0

b y = - a x

y = - a b x

x , y = x , - a b x = x 1 , - a b

O vetor diretor pode ser 1 , - a b ou qualquer múltiplo dele, como ( b , - a ) ou - b ,   a .

Passo 2

Vamos ver agora as afirmativas:

I -   A projeção ortogonal do vetor na reta é igual a projeção ortogonal do vetor no vetor diretor da reta, mas a ,   b não é múltiplo de 1 , - a b , logo, ele não vai ser diretor da reta e portanto essa afirmativa está incorreta.

I I - Primeiro, lembrando que - b , a é um vetor na direção da reta, vamos analisar o que tá acontecendo escolhendo um v → qualquer:

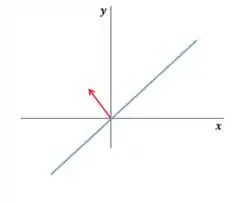
Vou refletir em r :

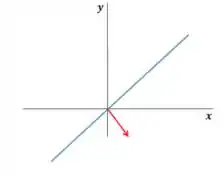
Ele tá me falando que isso daí deve ser igual a menos a projeção de v → em ( - b , a ) , ou seja, em r . Mas a projeção de v → em r é nula por ser ortogonal!

Logo não podem ser iguais e a afirmativa também vai ser falsa.

Resposta

a