UFRJ, Álgebra Linear, P4 – 2017.1, Questão 1
Seja uma reta de que passa pela origem e seja a matriz que representa a projeção ortogonal sobre seguida da reflexão pelo complemento ortogonal de . Considere as afirmativas abaixo:
é uma matriz simétrica
O núcleo de é o complemento ortogonal da imagem de
(a) Ambas são verdadeiras
(b) é falsa e é verdadeira
(c) é verdadeira e é falsa
(d) Ambas são falsas
Passo 1
Bom, primeira coisa que temos que saber é que uma matriz projeção sempre vai ser simétrica.
A nossa matriz vai ser a composição dessa matriz projeção com uma reflexão. O que acontece é o seguinte:
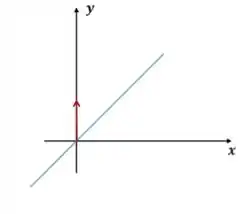
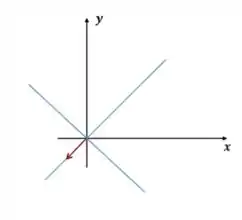
Reparem que quando eu refleti, o vetor foi apenas invertido, ou seja, se era virou
Assim, os vetores da imagem da minha matriz projeção vão mudar de sinal para virar a matriz
E assim minha matriz continua simétrica, então a afirmativa é verdadeira.
Passo 2
Bom, o núcleo de vai ser a reta ortogonal a reta pois como todos os vetores nele são perpendiculares, as projeções vão ser nulas!
E a imagem de são todos os vetores que obtivemos após a aplicação de , com o esqueminha que mostrei ali em cima, vemos que é a própria reta
Logo, essa segunda afirmativa é verdadeira!
Resposta
a