UFRJ, Álgebra Linear, P4 – 2017.1, Questão 03
Seja um subespaço não trivial de . Sejam e respectivamente a projeção e a reflexão ortogonais com respeito a
é ortogonal a
é ortogonal a
(a) Ambas são falsas
(b) é falsa e é verdadeira
(c)Ambas são verdadeiras
(d)é verdadeira e �� falsa
Passo 1
Vamos imaginar uma situação em que estamos no e é uma reta:
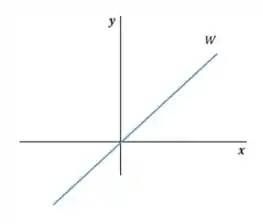
Agora vou analisar as duas situações escolhendo quaisquer
Passo 2
Vamos testar a primeira afirmativa, considerando esse e portanto, tendo a seguinte projeção:
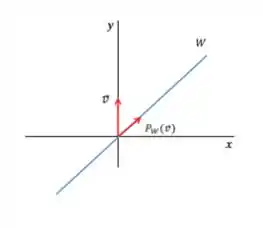
Agora basta achar e ver se ele é ortogonal à projeção:
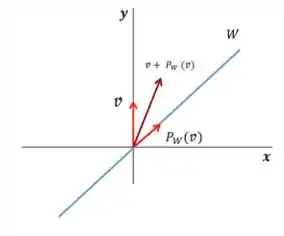
Opa, eles não são ortogonais!! Logo a afirmativa é falsa. Reparem que o que a gente acabou de fazer foi achar um contraexemplo para provar o que queríamos.
Passo 3
Agora vamos ver a segunda afirmativa, vou escolher meu assim:
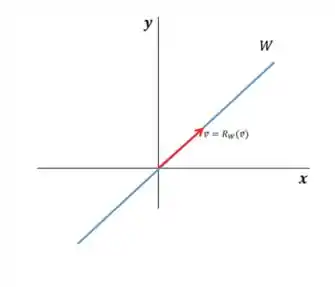
Agora vamos analisar se é ortogonal a
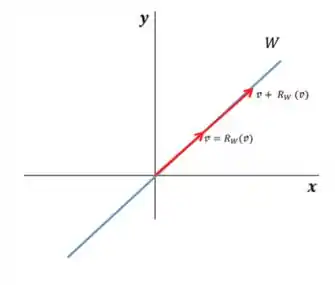
Claramente não serão ortogonais então essa afirmativa também é falsa!
Resposta
a