Responde Aí
Acesse com GoogleAcesse com AppleAcesse com Facebook

Exercícios Resolvidos de Relatividade do Tempo

Ver Teoria
Exercício 81234567910111213141516171819

Enunciado

PUC, Física 4, P2 2016.2, 3

A partir dos princípios da Relatividade Restrita obtenha a relação entre o tempo próprio medido por um observador que se move com velocidade relativística em relação a outro referencial e o intervalo de tempo medido pelo observador no outro referencial (dito estacionário).

Passo 1

Vamos analisar primeiro o referencial de quem está se movendo, ou seja, dentro do vagão, juntamente com isso faremos uma analise de um evento de luz nos dois referencias estudados, mas primeiro vamos analisar o referencial em que o evento ocorre.

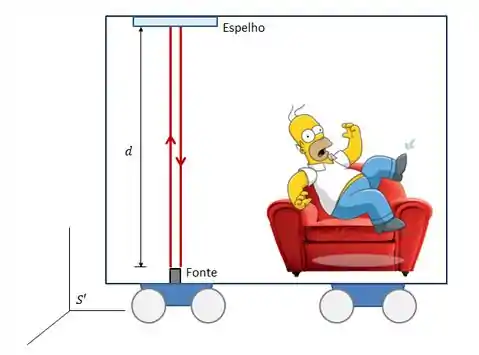
O tempo ∆ t 0 medido por Homer no dois eventos é dado pela relação

∆ t 0 = 2 d c

Em que o tamanho do vagão é d e c é a velocidade da luz

Passo 2

Vamos analisar agora o referencial de quem está fora do referencial em que ocorre o evento, ou seja, no nosso caso o referencial de quem está fora do vagão.

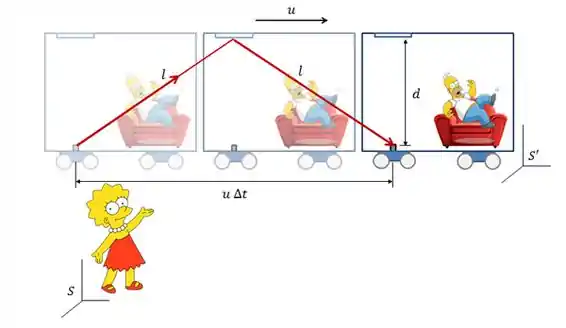
Nesse caso podemos dizer que o tempo medido pela Lisa pode ser descrito pela fórmula

∆ t = 2 l c

Usando Pitágoras podemos escrever a nossa fórmula do seguinte jeito

l = d 2 + u . ∆ t 2 2

∆ t = 2 c d 2 + u . ∆ t 2 2

Passo 3

Agora temos duas fórmulas que podemos relacionar

∆ t = 2 c d 2 + u . ∆ t 2 2

∆ t 0 = 2 d c

Isolando d e relacionando as fórmulas teremos

d = c . ∆ t 0 2

∆ t = 2 c c . ∆ t 0 2 2 + u . ∆ t 2 2

Fazendo as transformações algébricas e mudanças teremos a seguinte

c . ∆ t 2 2 = c . ∆ t 0 2 2 + u . ∆ t 2 2

c . ∆ t 2 - u . ∆ t 2 = c . ∆ t 0 2

∆ t 2 ( c 2 - u 2 ) = c 2 . ∆ t 0 2

Isolando ∆ t teremos

∆ t 2 = c 2 . ∆ t 0 2 ( c 2 - u 2 )

∆ t 2 = ∆ t 0 2 ( c 2 - u 2 c 2 )

∆ t = ∆ t 0 1 - u c 2

Resposta

∆ t = ∆ t 0 1 - u c 2

Exercícios de Livros Relacionados

52. Uma sonda espacial é enviada para a estrela Capella, situada a uma distância igual a 42,2 anos-luz da Terra. (Um ano-luz é a distância percorrida pela luz durante um ano.) A sonda se desloca com v
Se um avião voa a uma velocidade de 2.000 km / h, quanto tempo ele deve voar antes que seu relógio perca 1,00 s por causa da dilatação do tempo? (Dica: use um ou mais dos resultados do Problema 10.)
A que velocidade um relógio se move se ele funciona a uma taxa de metade da taxa de um relógio em repouso em relação a um observador?
Um astronauta está viajando em um veículo espacial que se move a 0,500 c em relação à Terra. Ele mede sua frequência cardíaca, cujo valor é 75,0 batidas por minuto. Os sinais gerados pelo seu pulso sã
Uma sonda espacial interestelar é lançada da Terra. Depois de um breve período de aceleração, ela se move a uma velocidade constante, com um módulo de 70,0 % da velocidade da luz. Suas baterias de com