Cada uma de 3 caixas possui 2 gavetas. A primeira caixa contém uma moeda de ouro em cada gaveta, a segunda caixa contém 2 moedas de prata em cada gaveta, e a terceira caixa, uma moeda de ouro em uma gaveta, e uma de prata na outra. Uma caixa é escolhida ao acaso; uma de suas gavetas é escolhida ao acaso e aberta, encontrando-se uma moeda de ouro. Qual a probabilidade que a moeda da outra gaveta seja também de ouro?
Passo 1
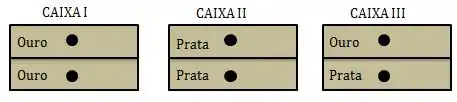
Vamos chamar de:
Passo 2
Usando probabilidade condicional a gente sabe que a probabilidade da segunda moeda ser de ouro sabendo que a primeira já foi de ouro é dada pela fórmula:
E é exatamente isso que a gente precisa calcular.
Passo 3
Vamos por partes.
é a probabilidade da primeira e da segunda moeda serem de ouro, certo?
Só que isso só acontece se escolherem a caixa I, concorda?
Então:
Passo 4
Agora temos que calcular a probabilidade da primeira moeda ser de ouro.
Pra isso, vamos usar o teorema da probabilidade total.
Probabilidade da primeira moeda ser de ouro é a prob. da primeira ser de ouro sabendo que escolhemos a caixa I vezes a probabilidade de escolhermos a caixa I, mais a prob. da primeira ser de ouro sabendo que escolhemos a caixa II vezes a prob. de escolhermos a caixa II e a mesma coisa pra III.
Como todas as moedas da caixa I são de ouro
Como na II não temos moedas de ouro
E na III temos uma de ouro
E a probabilidade de ser escolher qualquer caixa é:
Passo 5
Agora só substituir na fórmula:
E:
Que era exatamente o que a gente queria.