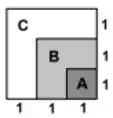
Um terreno quadrado de área apresenta três tipos de solo: , e , de acordo com a ilustração abaixo. Sabe-se que a chance de uma semente conseguir germinar no solo é , no solo é de e no solo é 20%. Além disso, assuma que a probabilidade de que uma semente levada pelo vento até esse terreno caia em cada um dos tipos de solo é proporcional a sua área.
- Calcule a probabilidade de que um semente que caia nesse terreno consiga germinar.
- Considerando que duas sementes caiam nesse terreno (de forma independente), calcule a probabilidade de que elas caiam em solos tipos diferentes.
- Considere agora que as duas sementes caíram no mesmo tipo de solo e que, posteriormente, observou-se que ambas conseguiram germinar. Calcule qual a probabilidade de que o solo em que elas caíram seja do tipo A.
Passo 1
Primeira coisa que precisamos determinar nesse problema é a probabilidade de uma semente cair em cada um desses terrenos. Visto isso podemos criar um mapa ilustratório que nos ajudar a identificar todas as possibilidade/probabilidades.
Por fim não devemos lembrar o Teorema de Bayes, onde
Não se preocupe caso você não lembre como aplicar o teorema, iremos fazer com cuidado a utilização dele ao longo do problema.
Passo 2
(a) Primeiro vamos olhar pra o nosso terreno e observar que a probabilidade de uma semente cair dele com a ação do vento está relacionado com a área do nosso terreno. Assim seja
Agora que já sabemos a probabilidade de uma semente encontrar cada um dos terrenos, vamos fazer um mapa sobre todas as probabilidades
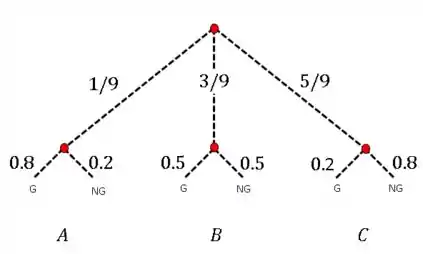
Onde aqui temos os 3 terrenos e as probabilidades em cada um deles de Germinar(G) e não Germinar (ND).
Agora queremos saber, qual a probabilidade de uma semente cair em qualquer um desses terrenos e ainda Germinar.
Pois bem, queremos saber então
Que são as probabilidade são as probabilidades delas caírem em cada terreno e germinar somadas.
Usando nosso mapa de probabilidade, temos que
E como sabemos todos os valores, podemos somente calcular, ou seja
Passo 3
(b) Vamos trabalhar na lógica para responder nosso problema. Queremos a probabilidade de duas sementes caírem em dois solos distintos de forma independente. E se a gente calcular a probabilidade delas caírem em solos iguais e tomar que , onde é a probabilidade de caírem em solos distintos e de cair em solos iguais.
Perceba que nossa tática torna o problema mais fácil de ser resolvido. Isso porque, como são eventos distintos, temos que a probabilidade de cair duas sementes em um mesmo solo é o produto das probabilidades, ou seja, a probabilidade de duas sementes caírem no solo A será
Assim podemos dizer então que
Que é igual a
Desta forma podemos dizer então que a probabilidade de duas sementes caírem em solos distinto é de
Passo 4
(c) Chegamos no ultimo item precisando usar o que dissemos que iriamos usar né hahah se falamos ...
Supondo que sabemos que duas partículas caíram no mesmo solo e germinaram, qual é a probabilidade de elas serem do solo , pois bem, então definimos que nossa probabilidade é descrita como
Onde é como iremos denotar quando as duas sementes germinaram e pos caírem no mesmo solo. Assim pelo Teorema de Bayes, temos que
Na qual é a probabilidade de duas sementes caírem no solo .
Ainda utilizando o Teorema de Bayes iremos fazer o calculo de , assim temos que
é a probabilidade de duas sementes caírem no solo sobre a probabilididade de duas sementes caírem sobre o mesmo solo. Sendo assim
e
E por fim, mas não menos importante, na verdade ainda muito importante, a probabilidade de duas sementes germinarem e pertecerem ao mesmo solo, ou seja
Perceba que como são eventos distintos, ou seja, uma semente não depende da outra, vale a regra da multiplicação de probabilidades. Seguindo o mesmo raciocínio pra os outros solos
e
Isso quer dizer que, se duas sementes caírem em um desses solos, essa é a probabilidade de elas ambas conseguirem germinar.
Assim temos elementos para finalizar nosso calculo, ou seja
Meu deus ... que questão. Isso em uma prova é bem triste.