O funcionamento do sistema ilustrado abaixo depende de 5 componentes: . Cada um desses componentes tem probabilidade 0,1 de estar defeituoso, independente dos demais; e o sistema irá funcionar apenas se houver pelo menos um caminho conectando os pontos A e B ao longo do qual nenhum componente esteja defeituoso.

a) Calcule a probabilidade de que pelo menos um dos 5 componentes esteja defeituoso.
b) Calcule a probabilidade desse sistema funcionar.
c) Calcule a probabilida de que o componente esteja defeituoso, dado que o sistema está funcionando.
Passo 1
a) Calcule a probabilidade de que pelo menos um dos 5 componentes esteja defeituoso
Queremos a probabilidade de PELO MENOS um dos 5 estar com defeito. Esse pelo menos aí tem que nos lembrar daquele bizu do complementar. Lembram?
P( pelo menos um dos 5 estar com defeito) = 1- P(nenhum ter defeito)
Então vamos calcular essa probabilidade:
Passo 2
Como estamos falando de eventos independentes, podemos falar que:
Pelo enunciado sabemos que:
Então
Como a probabilidade é igual para todos os componentes, teremos
Passo 3
Assim, substituindo teremos:
Passo 4
b) Calcule a probabilidade desse sistema funcionar.
O enunciado nos diz: “o sistema irá funcionar apenas se houver pelo menos um caminho conectando os pontos A e B ao longo do qual nenhum componente esteja defeituoso.”
Então temos que olhar o desenho e analisar os caminhos:

1ª observação: Tanto o componente quanto o não podem estar com defeito, pois caso estejam não teremos um caminho ligando A e B.
A partir disso teremos algumas opções:
1ª opção: O componente está com defeito e estão funcionando
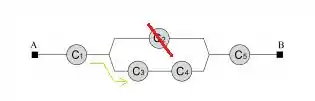
2ª opção: O componente está funcionando e estão com defeito.
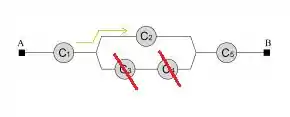
3ª opção: O componente estão funcionando e está com defeito. (O caminho realizado será pelo fio de cima.)
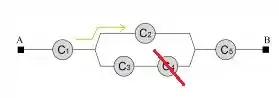
4ª opção: O componente estão funcionando e está com defeito. (O caminho realizado será pelo fio de cima)
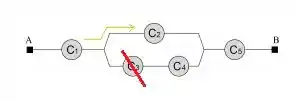
5ª opção: Todos os componente estão funcionando.

Simbora calcular a probabilidade de cada opção?
Passo 5
1ª opção: O componente está com defeito e estão funcionando
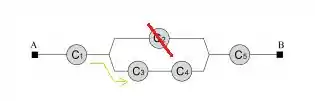
Funcionando:
Não funcionando:
Queremos:
Passo 6
2ª opção: O componente está funcionando e estão com defeito.
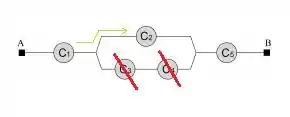
Funcionando:
Não funcionando:
Queremos:
Passo 7
3ª opção: O componente estão funcionando e está com defeito. (O caminho realizado será pelo fio de cima.)
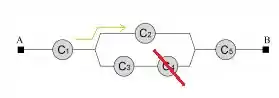
Funcionando:
Não funcionando:
Queremos:
Passo 8
4ª opção: O componente estão funcionando e está com defeito. (O caminho realizado será pelo fio de cima)
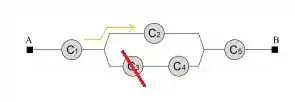
Funcionando:
Não funcionando:
Queremos:
Passo 9
5ª opção: Todos os componente estão funcionando.

Funcionando:
Não funcionando:
Queremos:
Passo 10
Como dividimos em várias opções, devemos somar esses resultados:
Passo 11
c) Calcule a probabilidade de que o componente esteja defeituoso, dado que o sistema está funcionando.
Agora estamos falando de condicional certo? E como que sabemos isso? Bom, ele está pedindo a probabilida de que seja defeituoso DADO QUE o sistema está funcionando. Ou seja, ele já está afirmando que o sistema funciona!
Escrevendo a fórmula da condicional:
Bom, nós acabamos de calcular no item (B)... Agora devemos focar no cálculo de .
Passo 12
Para calcularmos precisamos entender o que é esse termo.
Queremos a probabilidade de falhar e o experimento funcionar. Vamos olhar lá para as nossas opções do item B e verificar quais se enquadram nisso:
2ª opção: O componente está funcionando e estão com defeito.
4ª opção: O componente estão funcionando e está com defeito.
Então podemos falar que:
Passo 13
Substituindo teremos:
Resposta
a)
b)
c)