Responde Aí
Acesse com GoogleAcesse com AppleAcesse com Facebook

Exercícios Resolvidos de Teorema de Laplace

Ver Teoria
Exercício 1412345678910111213

Enunciado

UFRJ, P4-2019.2

Calcule o determinante da matriz:

A = 2 0 0 1 1 4 1 0 2 3 4 5 1 2 3 1 0 0 1 1 1 0 0 1 3

  1. - 3
  2. - 2
  3. 2
  4. 3

Passo 1

Belezera galerinha, temos uma matriz GIGANTESCA 5 × 5 e queremos descobrir o determinante dessa coisa linda.

Maass calma lá, porque tá vendo ali que temos a terceira coluna quase que inteira formada de zeros!! Isso é uma dica pra gente usar Laplace nessa coluna, saca só:

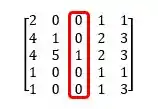
Então se a gente aplicar Laplace com essa coluna de guia, vamos obter:

det ⁡ 2 0 0 1 1 4 1 0 2 3 4 5 1 2 3 1 0 0 1 1 1 0 0 1 3 = det ⁡ - 1 3 + 3 1 2 0 1 1 4 1 2 3 1 0 1 1 1 0 1 3

det ⁡ 2 0 0 1 1 4 1 0 2 3 4 5 1 2 3 1 0 0 1 1 1 0 0 1 3 = det ⁡ 2 0 1 1 4 1 2 3 1 0 1 1 1 0 1 3

Passo 2

E agora a gente pode aplicar mais uma vez Laplace, só que agora na segunda coluna da matriz:

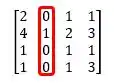
Logo, o determinante dessa matriz é:

det ⁡ 2 0 1 1 4 1 2 3 1 0 1 1 1 0 1 3 = det ⁡ - 1 2 + 2 1 2 1 1 1 1 1 1 1 3

det ⁡ 2 0 1 1 4 1 2 3 1 0 1 1 1 0 1 3 = det ⁡ 2 1 1 1 1 1 1 1 3

E agora ficou xuxu beleza, é só a gente calcular o determinante de 2 1 1 1 1 1 1 1 3 . A gente pode aplicar Regra de Sarrus, desse jeito:

det ⁡ 2 1 1 1 1 1 1 1 3 = 2 1 1 1 1 1 1 1 3 2 1 1 1 1 1 = 6 + 1 + 1 - 3 + 2 + 1

det ⁡ 2 1 1 1 1 1 1 1 3 = 2

Portanto:

det ⁡ 2 0 0 1 1 4 1 0 2 3 4 5 1 2 3 1 0 0 1 1 1 0 0 1 3 = 2

E nossa resposta certa é a letra (c).

Resposta

Letra (c)

Exercícios de Livros Relacionados

Calcule os cofatores de cada um dos termos da matriz A = 1 2 1 0 1 2 2 3 1
Calcular o cofator do elemento x da matrizA = ([[[[[[0,1]],[[0,3]]]]],[[[[[1,2]],[[1,1]]]]],[[[[[2,1]],[[0,0]]]]],[[[[[3,x]],[[2,1]]]]]])
Desenvolva pela primeira coluna det ⁡ A = ∑ i = 1 3 a i 1 A i 1 e depois calcule o determinante da matriz 3 4 0 1 1 0 2 0 2
Repetir o exercício 3 com a matriz([[2,1,3,0],[1,2,1,0],[0,0,2,1],[3,1,1,4]])
Sejam A , B e C matrizes de ordem 2 e seja X = A C 0 B De ordem 4. Provar que det ⁡ X = det ⁡ A det ⁡ B . Este resultado vale para A , B , C ∈ M n R .