Responde Aí
Acesse com GoogleAcesse com AppleAcesse com Facebook

Exercícios Resolvidos de Alterações na Mudança de Variável

Ver Teoria
Exercício 1212345678910111314151617181920

Enunciado

Calcule a integral ∭ W 7 x 2 + 21 y 2 d V , onde W é o sólido limitado pelas superfícies z = 2 x 2 + 2 y 2 - 1 e z = x 2 - y 2

Passo 1

Bom, aqui pra calcular a integral tripla vai ajudar bastante se fizermos coordenadas cilíndricas. Pra descobrir a projeção do sólido no plano x y , vamos igualar as duas equações do enunciado, olha só:

z = 2 x 2 + 2 y 2 - 1

z = x 2 - y 2

2 x 2 + 2 y 2 - 1 = x 2 - y 2

x 2 + 3 y 2 = 1

Isso aí em coordenadas cilíndricas fica assim

x 2 = r 2 cos 2 ⁡ θ

x = r cos ⁡ θ

3 y 2 = r 2 sen 2 ⁡ θ

y = r sen ⁡ θ 3

O jacobiano aqui é aquele de mudança elíptica lá de integrais duplas, lembra?

J = a b r

J = r 3

Onde

0 ≤ r ≤ 1

0 ≤ θ ≤ 2 π

Já que estamos fazendo coordenadas cilíndricas, precisamos ainda dos limites de z , certo? Mas quem é o limite inferior e o superior? Vamos analisar as duas equações:

Quando r = 0 , temos que x = 0 e y = 0 . Nesse ponto

z = 2 x 2 + 2 y 2 - 1

z = - 1

A segunda equação

z = x 2 - y 2

z = 0

Portanto a equação z = 2 x 2 + 2 y 2 - 1 é o limite inferior e z = x 2 - y 2 é o limite superior. Se você não gostou dessa lógica, o esboço do sólido é esse aqui:

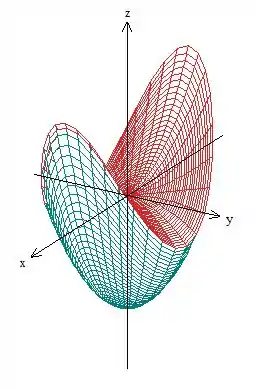
Onde o paraboloide de baixo é z = 2 x 2 + 2 y 2 - 1 e a superfície vermelha de cima é a sela z = x 2 - y 2 . Logo:

2 x 2 + 2 y 2 - 1 ≥ z ≥ x 2 - y 2

Mas sabemos que x = r cos ⁡ θ e y = r sen ⁡ θ 3 , logo

2 r cos ⁡ θ 2 + 2 r sen ⁡ θ 3   2 - 1 ≥ z ≥ r cos ⁡ θ 2 - r sen ⁡ θ 3 2

2 r 2 cos 2 ⁡ θ + 2 3 r 2 sen 2 ⁡ θ - 1 ≥ z ≥ r 2 cos 2 ⁡ θ - r 2 sen 2 ⁡ θ 3

Bem feio, né? Mas prometo que vai ficar melhor depois, continua comigo!!

Passo 2

Bom, vamos colocar isso na integral tripla

∭ W 7 x 2 + 21 y 2 d V

Esse cara dentro da integral tripla fica assim

7 x 2 + 21 y 2 = 7 r 2 cos 2 ⁡ θ + 21 r sen ⁡ θ 3 2

= 7 r 2 cos 2 ⁡ θ + 7 r 2 sen 2 ⁡ θ

= 7 r 2

Colocando os limites calculados no passo 1 e o jacobiano

= ∫ 0 2 π ∫ 0 1 ∫ 2 r 2 cos 2 ⁡ θ + 2 3 r 2 sen 2 ⁡ θ - 1 r 2 cos 2 ⁡ θ - r 2 sen 2 ⁡ θ 3 7 r 2 r 3 d z d r d θ

= ∫ 0 2 π ∫ 0 1 ∫ 2 r 2 cos 2 ⁡ θ + 2 3 r 2 sen 2 ⁡ θ - 1 r 2 cos 2 ⁡ θ - r 2 sen 2 ⁡ θ 3 7 r 3 3 d z d r d θ

Passo 3

Integrando em z isso aí

∫ 0 2 π ∫ 0 1 ∫ 2 r 2 cos 2 ⁡ θ + 2 3 r 2 sen 2 ⁡ θ - 1 r 2 cos 2 ⁡ θ - r 2 sen 2 ⁡ θ 3 7 r 3 3 d z d r d θ =

= ∫ 0 2 π ∫ 0 1 7 r 3 3 r 2 cos 2 ⁡ θ - r 2 sen 2 ⁡ θ 3 - 2 r 2 cos 2 ⁡ θ + 2 3 r 2 sen 2 ⁡ θ - 1 d r d θ

Agora é o momento que minha promessa vira verdade, olha só o que sobra nessa integral aí

= ∫ 0 2 π ∫ 0 1 7 r 3 3 - r 2 cos 2 ⁡ θ - r 2 sen 2 ⁡ θ + 1 d r d θ

= ∫ 0 2 π ∫ 0 1 7 r 3 3 1 - r 2 d r d θ

= 7 3 ∫ 0 2 π ∫ 0 1 r 3 - r 5 d r d θ

Integrando em r

= 7 3 ∫ 0 2 π r 4 4 - r 6 6 0 1 d θ

= 7 3 ∫ 0 2 π 1 4 - 1 6 d θ

= 7 3 ∫ 0 2 π 1 12 d θ

Por fim, integrando em θ

= 7 3 . 1 12 . 2 π = 7 π 6 3

= 7 3 π 18

Resposta

7 π 3 18