Responde Aí
Acesse com GoogleAcesse com AppleAcesse com Facebook

Exercícios Resolvidos de Alterações na Mudança de Variável

Ver Teoria
Exercício 6123457891011121314151617181920

Enunciado

Encontre o volume do elipsoide

x 2 a 2 + y 2 b 2 + z 2 c 2 = 1

(Sugestão: Sejam x = a u ,   y = b v ,   z = c w . Então encontre o volume sobre uma região apropriada no espaço u v w . )

Passo 1

Esse elipsoide tem a seguinte imagem,

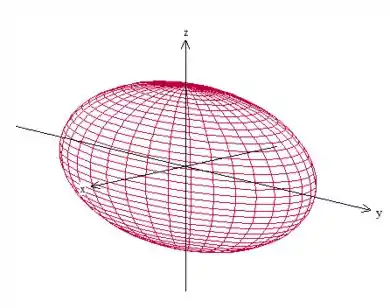
Veja que ele parece um pouco com uma esfera! Como queremos o volume do elipsoide, vamos resolver a integral

V = ∭ W   d x d y d z

A sugestão do exercício é de fazer a seguinte mudança de variáveis, x = a u ,   y = b v ,   z = c w , assim, o volume seria

V = ∭ W   d x d y d z = ∭ T J u , v , w d u d v d w

Para isso, precisamos calcular o jacobiano!

Passo 2

O jacobiano é calculado por,

J ( u ,   v , w ) = ∂ x , y , z ∂ ( u , v , w ) = d x d u d x d v d x d w d y d u d y d v d y d w d z d u d z d v d z d w

Como, x = a u ,   y = b v ,   z = c w

d x d u = a , d x d v = d x d w = 0

d y d u = 0 , d y d v = b , d y d w = 0

d z d u = 0 , d z d v = 0 , d z d w = c

Desta forma temos o determinante,

J u ,   v , w = a 0 0 0 b 0 0 0 c = a b c

Passo 3

Ao fazer esta mudança de variáveis nosso elipsoide fica com a forma,

a 2 u 2 a 2 + b 2 v 2 b 2 + c 2 w 2 c 2 = 1 → u 2 + v 2 + w 2 = 1

Ou seja, no espaço u v w , temos uma esfera de raio 1 .

Passo 4

Agora vamos ver como fica o volume V

V = ∭ W   d x d y d z = ∭ T J u , v , w d u d v d w

V = ∭ T ( a b c ) d u d v d w   = a b c ∭ T d u d v d w

Mas,

∭ T d u d v d w

É o volume do solído no espaço u v w , ou seja, o volume da esfera de raio 1 , assim

∭ T d u d v d w = 4 π 3

Logo,

V = a b c ⋅ 4 π 3

Resposta

V = a b c ⋅ 4 π 3