Responde Aí
Acesse com GoogleAcesse com AppleAcesse com Facebook

Exercícios Resolvidos de Alterações na Mudança de Variável

Ver Teoria
Exercício 2012345678910111213141516171819

Enunciado

Calcule a massa do sólido W situado no primeiro octante, limitado pelos planos x = 0 , y = 2 x e pelo cilindro y 2 + z 2 = 2 , supondo que a densidade no ponto x ,   y ,   z é proporcional à distância deste ponto ao plano x y .

Passo 1

Cara, massa de um sólido a essa altura do campeonato para a gente não é nada mais é do que uma integral tripla

M a s s a W = ∭ W δ x ,   y ,   z d V

Onde δ x ,   y ,   z é a função de densidade do sólido.

Mas aí surge duas duvidas não é verdade?!

  1. Quem é o sólido W que estamos trabalhando?
  2. Quem é a função δ x ,   y ,   z ?

Passo 2

Vamos começar aqui respondendo a primeira pergunta!

Bem, se você quer entender o sólido, desenhe, como sempre fazemos, essas superfícies delimitadoras juntas no espaço (primeiro octante), obtendo esse carinha apontado pela flecha aí oh!

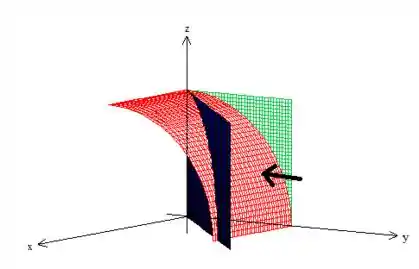
Passo 3

Pow! estamos dentro de um cilindro, então nada mais justo que pensarmos na mudança para coordenadas cilíndricas, certo?

Certo! Mas... cuidado, pois esse cilindro está ao redor de x e não de z , então vamos usar a mudança com esse pequeno grande detalhe:

x = x  

z = r cos ⁡ θ

y = r sin ⁡ θ

(Como se tivéssemos apenas trocado o x pelo z , pegou )

O J a c o b i a n o continua o mesmo

J = r

Passo 4

Como sempre, não podemos deixar de encontrar as variações dos novos caras, e vamos começar aqui por ele, o grande x

Bem, o x está variando lá de trás, até aqui na frente

P l a n o   V e r d e ≤ x ≤ P l a n o   A z u l

o plano a z u l é y = 2 x , logo...

0 ≤ x ≤ y 2

Sim, estamos em outras coordenadas agora, então

0 ≤ x ≤ r sin ⁡ θ 2

Enquanto ao θ , bem ele dá uma meia volta saindo do z e r o ali no eixo y

0 ≤ θ ≤ π 2

e o r varia da origem até o raio máximo do cilindro vermelho

0 ≤ r ≤ C i l i n d r o   V e r m e l h o

0 ≤ r ≤ 2

Passo 5

Wow! Yeah! A segunda pergunta...

  1. Quem é a função δ x ,   y ,   z ?

Bem... O próprio enunciado disse que a densidade é proporcional a distancia de um ponto ao plano x y . A distância a esse plano é o próprio valor de z , logo

δ x ,   y ,   z = k z

onde k é a constante de proporcionalidade, ok?

Mas... como estamos agora nas coordenadas cilindricas...

δ = k   r cos ⁡ θ

Passo 6

Bem, agora é só montar a integral tripla e correr para o abraço!

∭ W   δ ( x ,   y , z )   d V

Lembre-se de substituir pelas coordenadas cilíndricas e não deixar de multiplicar pelo J a c o b i a n o ;)

∫ 0 π 2 ∫ 0 2 ∫ 0 r sin ⁡ θ 2 k   r cos ⁡ θ   J   d x d r d θ =

∫ 0 π 2 ∫ 0 2 ∫ 0 r sin ⁡ θ 2 k   r 2 cos ⁡ θ   d x d r d θ

Calculando essa integral aí então começando pela de dentro em x , portanto considerando todos uma constante...

∫ 0 π 2 ∫ 0 2 k   r 2 cos ⁡ θ ∫ 0 r sin ⁡ θ 2   d x d r d θ =

∫ 0 π 2 ∫ 0 2 k   r 2 cos ⁡ θ x 0 r sin ⁡ θ 2 d r d θ =

∫ 0 π 2 ∫ 0 2 k   r 2 cos ⁡ θ r sin ⁡ θ 2 d r d θ = k 2 ∫ 0 π 2 ∫ 0 2 r 3 cos ⁡ θ sin ⁡ θ d r d θ =

Calculando agora a integral do meio...

k 2 ∫ 0 π 2 cos ⁡ θ sin ⁡ θ ∫ 0 2 r 3 d r d θ =

k 2 ∫ 0 π 2 cos ⁡ θ sin ⁡ θ r 4 4 0 2 d θ =

k 2 ∫ 0 π 2 cos ⁡ θ sin ⁡ θ d θ

Realizando uma mudança simples, integramos essa última aí

sin ⁡ θ = t       →           d t = cos ⁡ θ d θ

(troque também os limites de integração)

θ = 0           →               t = sin ⁡ 0 = 0

θ = π 2           →               t = sin ⁡ π 2 = 1

Retornando a integral, substituindo e calculando, concluímos que

k 2 ∫ 0 π 2 cos ⁡ θ sin ⁡ θ d θ = k 2 ∫ 0 1 t   d t =

k 2 t 2 2 0 1 = k 4

Resposta

k 4