Responde Aí
Acesse com GoogleAcesse com AppleAcesse com Facebook

Exercícios Resolvidos de Alterações na Mudança de Variável

Ver Teoria
Exercício 1512345678910111213141617181920

Enunciado

Questão 2: Calcule o volume do sólido delimitado por x 2 + 2 y 2 + 3 z 2 ≤ 4 , x ≥ 1 , y ≥ 0 , z ≥ 0 .

Passo 1

Então, se um problema nos pede volume, o que ele quer que façamos? SIM! Uma integral tripla:

V = ∭ S   1 d V

No caso, para resolvermos o nosso problema, precisamos o sólido S que buscamos o volume, e em seguida calcularmos tal integral. Vamos nessa?

Passo 2

Bem, para descrevermos o sólido S , seria muito interessante desenharmos primeiro tal sólido no espaço para termos uma noção geométrica do nosso problema. Então esse será o nosso segundo passo :

O nosso sólido é formado por basicamente por um elipsoide de equação x 2 + 2 y 2 + 3 z 2 = 4 . O seu desenho é esse daqui:

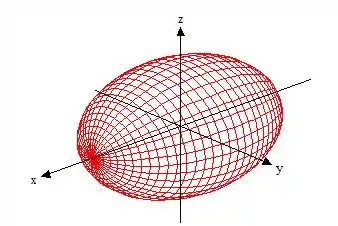
Só que queremos o sólido delimitado pelo plano x = 1 (onde x ≥ 1 ):

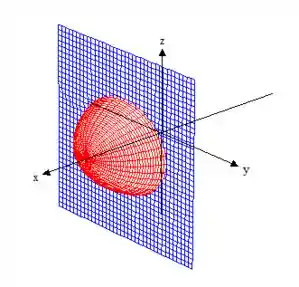
Por último, trata-se de um sólido que está nos primeiro octante, já que y ≥ 0 e z ≥ 0 :

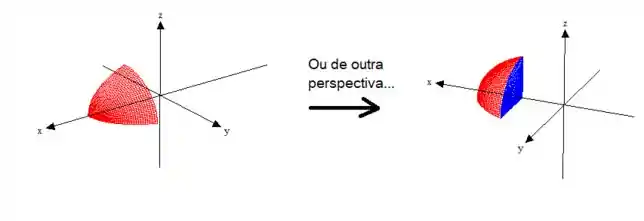
Lembre-se de que não se trata de um desenho perfeito, e sim apenas uma noção geométrica. Então, não se preocupe se o seu desenho não ficou assim ;)

Passo 3

Como estamos trabalhando com um elipsoide, acho interessante pensarmos em uma mudança para coordenadas elipsoidais ! Trata-se das coordenadas esféricas...

x = r ⋅ sin ⁡ φ ⋅ cos ⁡ θ

y = r ⋅ sin ⁡ φ ⋅ sin ⁡ θ

z = r ⋅ cos ⁡ φ

Só que a gente vai mudar algumas coisas nela. Bem, primeiro, perceba que com essa mudança, temos essas variáveis “variando” desse jeito aqui, veja:

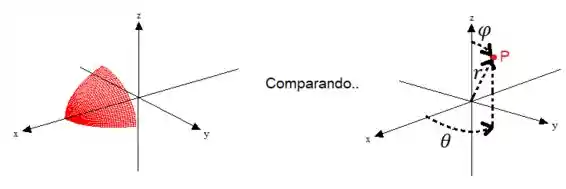
Poxa, veja que é extremamente complicado descrever o sólido com essas variáveis do jeito que esta, pois o ângulo φ é depende do ângulo θ . Mas veja que se mudarmos as coordenadas de forma que o ângulo φ varie de 0 até a borda feita pelo plano x = 1 , dessa forma aqui:

Muito melhor, pois assim, o ângulo θ varia de 0 até 90 ° , enquanto ângulo φ varia de 0 até a borda com o plano x = 1 sem depender de θ , saca? Mas ao fazer essa mudança, estamos basicamente mudando as coordenadas:

x = r ⋅ sin ⁡ φ ⋅ cos ⁡ θ y = r ⋅ sin ⁡ φ ⋅ sin ⁡ θ = r ⋅ cos ⁡ φ                               P a s s a   a   s e r … →                             y = r ⋅ sin ⁡ φ ⋅ cos ⁡ θ z = r ⋅ sin ⁡ φ ⋅ sin ⁡ θ x = r ⋅ cos ⁡ φ

Pra fazer essa troca, é só observar que para o ângulo φ sai do eixo x , então temos que ter o cos ⁡ φ com x (o mesmo vale para o ângulo θ sai do eixo y ), saca?

Outra coisa importante nas mudanças que iremos utilizar, é que essas acima são para esferas! Para elipsoides, devemos levar a equação do paraboloide para a equação geral dele...

x 2 + 2 y 2 + 3 z 2 = 4                   →                           x 2 4 + y 2 2 + z 2 4 3 = 1             →

x 2 2 2 + y 2 2 2 + z 2 2 / 3 = 1

Agora a gente faz essa mudança aqui:

  y = r ⋅ sin ⁡ φ ⋅ cos ⁡ θ z = r ⋅ sin ⁡ φ ⋅ sin ⁡ θ x = r ⋅ cos ⁡ φ                     →                 y = 2   r ⋅ sin ⁡ φ ⋅ cos ⁡ θ z = 2 3 r ⋅ sin ⁡ φ ⋅ sin ⁡ θ x = 2 ⋅ r ⋅ cos ⁡ φ

O Jacobiano dessa mudança é o produto desses números pelo jacobiano das mudanças esféricas:

J = 2 ⋅ 2 3 ⋅ 2 ⋅ r 2 sin ⁡ φ = 4 6 3 r 2 sin ⁡ φ

Passo 4

Com isso estamos preparados para encontrar agora os limites das variáveis r ,   θ   e   φ . O de θ , já até comentamos que na mudança que a gente fez varia de 0 até 90 ° quando ele bate na parede formada pelo plano x z :

0 ≤ θ ≤ π 2

Enquanto isso, o r varia do plano x = 1 até o elipsoide:

P a r e d e   ( x = 1 ) ≤ r ≤ E l i p s o i d e

E o φ varia de 0 (eixo x ) até a intersecção com a parede x = 1 :

0 ≤ φ ≤ I n t e r s e c ç ã o   c o m   a   P a r e d e   ( x = 1 )

Primeiro, vamos entender o que é o Elipsoide para o limite do raio: o elipsoide tem equação:

x 2 2 2 + y 2 2 2 + z 2 2 / 3 = 1

E se substituirmos as coordenadas que escolhemos, vamos encontrar:

r 2 = 1     →

r = 1

Isso é verdade, pois as coordenadas escolhidas no passo anterior foi através da equação do elipsoide, saca? Então...

P a r e d e   ( x = 1 ) ≤ r ≤ 1

Agora, vamos entender quem é a variação do raio na parede x = 1 . Substituindo as coordenadas elipsoidais escolhidas:

x = 1       →

2 ⋅ r ⋅ cos ⁡ φ = 1       →

r = 1 2 cos ⁡ φ

Então...

1 2 cos ⁡ φ ≤ r ≤ 1

Para encontrar a variação do ângulo φ :

0 ≤ φ ≤ I n t e r s e c ç ã o   c o m   a   P a r e d e   x = 1

Veja então que o raio máximo acontece na intercessão do elipsoide de r = 1 com o plano x = 1 ...

x = 1       →

2 ⋅ r ⋅ cos ⁡ φ = 1       →

2 ⋅ 1 ⋅ cos ⁡ φ = 1           →

cos ⁡ φ = 1 2

Qual é o ângulo cujo cosseno é 1 / 2 ? SIM! 60 ° ! Ou em Radianos π / 3 :

0 ≤ φ ≤ π 3

Concluímos então que as três variações são:

0 ≤ θ ≤ π 2 0 ≤ φ ≤ π 3 1 2 cos ⁡ φ ≤ r ≤ 1

Passo 5

Agora, finalmente, podemos retornar para a integral que calcula o volume:

V = ∭ S   1 d V

E, lembrando-se do Jacobiano, substituir as coordenadas:

V = ∫ 0 π 2 ∫ 0 π 3 ∫ 1 2 cos ⁡ φ 1 1 ⋅ J   d r d φ d θ =

∫ 0 π 2 ∫ 0 π 3 ∫ 1 2 cos ⁡ φ 1 4 6 3 r 2 sin ⁡ φ   d r d φ d θ

Calculando então as integrais:

4 6 3 ∫ 0 π 2 ∫ 0 π 3 sin ⁡ φ ∫ 1 2 cos ⁡ φ 1 r 2   d r d φ d θ = 4 6 3 ∫ 0 π 2 ∫ 0 π 3 sin ⁡ φ r 3 3 1 2 cos ⁡ φ 1 d φ d θ =

4 6 3 ∫ 0 π 2 ∫ 0 π 3 sin ⁡ φ 1 3 - 1 2 cos ⁡ φ 3 3 d φ d θ = 4 6 3 ∫ 0 π 2 ∫ 0 π 3 sin ⁡ φ 1 3 - 1 24 cos 3 ⁡ φ d φ d θ

Fazendo uma mudança tal que cos ⁡ φ = t , tal que:

d t = - sin ⁡ φ d φ         o u             sin ⁡ φ d φ = - d t

Trocando também os limites de φ pelos de t ...

φ = 0               →               t = cos ⁡ 0 = 1

φ = π 3               →               t = cos ⁡ π 3 = 1 2

4 6 3 ∫ 0 π 2 ∫ 0 π 3 sin ⁡ φ 1 3 - 1 24 cos 3 ⁡ φ d φ d θ = 4 6 3 ∫ 0 π 2 ∫ 1 1 / 2 1 3 - 1 24 t 3 - d t d θ =

Mudando também a ordem de integração com o sinal:

4 6 3 ∫ 0 π 2 ∫ 1 2 1 1 3 - 1 24 t 3 d t d θ = 4 6 3 ∫ 0 π 2 1 3 t + 1 48 t 2 1 2 1 d θ =

4 6 3 ∫ 0 π 2 1 3 + 1 48 - 1 3 1 2 + 1 48 1 / 2 2 d θ =

4 6 3 ∫ 0 π 2 1 3 + 1 4 8 - 1 6 + 1 1 2 d θ = 17 48 - 3 12 ⋅ 4 6 3 ∫ 0 π 2 d θ =

5 48 ⋅ 4 6 3 ⋅ π 2 =

5 π 6 72

Resposta

5 π 6 72