Questão 1:
Seja o sólido definido pela intersecção das esferas: e . Calcule o volume de .
Passo 1
Então, o cálculo do volume de para a gente aqui é dado por uma integral tripla:
Uma integral tripla até simpática, neh? O nosso trabalho central aqui, antes da calcular a integral, é descrever o sólido . Em falar nisso... Quem é o sólido ? Vem comigo descobrir ;)
Passo 2
Bem, pelo enunciado, o sólido é o que esta na intersecção de duas esferas de raio ... Uma está deslocada unidades para o lado direito em , e a outra duas unidades pra esquerda da origem:
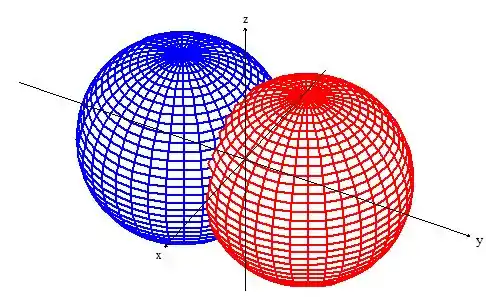
Muitas vezes é interessante enxergar essa intersecção como uma secção plana, já que é um sólido simétrico...
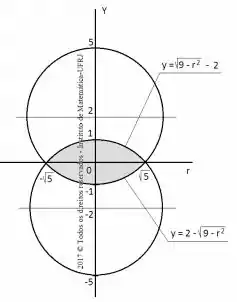
Eis o sólido, como se fosse uma ostra virada, sacou?
Passo 3
Ok, sabemos quem é o sólido, mas agora como podemos descrevê-lo?
Veja que embora ele esteja dentro de esferas, descrevê-lo em coordenadas esféricas não seria uma boa ideia, pois as esferas não estão centradas no mesmo lugar.
Agora, note que conseguimos colocar essa “concha do mar” dentro de um cilindro ao redor de :
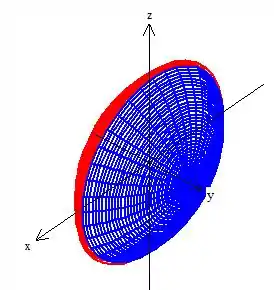
Sugerindo que mudemos para as coordenadas cilíndricas alterada (alterada, pois é em torno de , e não de como estamos acostumados):
O continua sendo ...
Uma equação que ajuda muito é a equação do cilindro...
Nunca terminamos uma mudança dessas sem dizer onde os parâmetros variam, então...
Passo 4
Para encontrar os limites do raio e , seria muito legal se conseguíssemos saber qual é o raio daquele cilindro que circunda a região , neh?
Note que ambas as esferas se encontram em , então substituindo na equação de uma das esferas...
Ou seja, o cilindro que circunda o sólido é um cilindro de raio igual a , logo o raio no sólido varia de até esse raio máximo...
Quanto ao , bem, a superfície dá uma volta completa ao redor de , o que significa que ele varia de...
Passo 5
Quanto ao limite da última variável, o próprio , repare que ele está variando da calota da esfera vermelha, até a calota da azul...
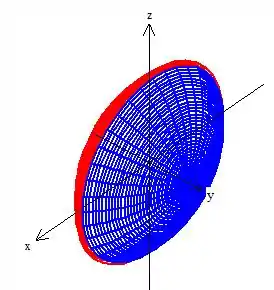
A calota azul é gerada da esfera...
Como estamos do lado direito da esfera azul, pegamos a raiz positiva mesmo...
Fazendo o mesmo para a calota da vermelha, já que a esfera vermelha é...
Agora aqui, veja que em relação ao centro da esfera vermelha, pegamos a calota a esquerda, por isso o negativo na raiz, saca?
Mudando para as coordenadas cilíndricas que estamos trabalhando...
Passo 6
Pegando essas três variações...
E substituindo na integral tripla do volume...
Não se esqueça do jacobiano!
Integrando...
Calculando a primeira integral fazendo uma mudança...
Mudando também os limites...
Calculando a outra integral dupla...
Logo...