Responde Aí
Acesse com GoogleAcesse com AppleAcesse com Facebook

Exercícios Resolvidos de Alterações na Mudança de Variável

Ver Teoria
Exercício 1012345678911121314151617181920

Enunciado

  1. Calcule a massa do sólido limitado pelo plano z = 0 , o cilindro x 2 + y 2 = 2 x e pelo cone z = x 2 + y 2 , se a densidade é ρ x ,   y ,   z = x 2 + y 2 .

Passo 1

Cara, massa de um sólido a essa altura do campeonato para a gente não é nada mais é do que uma integral tripla

M a s s a W = ∭ W ρ x ,   y ,   z d V

Onde já temos a função de densidade ρ x ,   y ,   z = z . Mas aí surge uma duvida:

  • Quem é o sólido W que estamos trabalhando?

Passo 2

Vamos começar aqui respondendo a primeira pergunta!

Pow, que o sólido é limitado pelo cone z = x 2 + y 2

acima do plano z = 0 , disso já sabemos. Mas agora quem é esse cilindro aqui: x 2 + y 2 = 2 x ?

Cara, uma dica para você é que toda vez que você ver esse tipo de cilindro, se trata de um cilindro com o eixo deslocado, veja...

Podemos passar esse menos 2 x para o lado de lá...

x 2 - 2 x + y 2 = 0         →                  

e sabendo que x - 1 2 = x 2 - 2 x + 1 (isso que é o completar quadrado ):

x - 1 2 - 1 + y 2 = 0         →                                  

x - 1 2 + y 2 = 1  

Viu só? É um cilindro de raio 1 com o eixo descolocado uma unidade em x ! Nos dando então esse sólido aqui apontado por essa flexa!

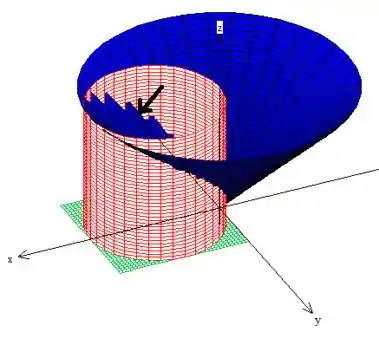
Passo 3

Pow! estamos dentro de um cilindro, então nada mais justo que pensarmos na mudança para coordenadas cilíndricas, certo?

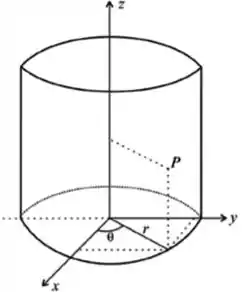
Então aqui la vai a troca

x = r cos ⁡ θ  

y = r sin ⁡ θ

z = z

O J a c o b i a n o dessa mudança é

J = r

e uma equação que nos ajuda, tipo, muuuuuito é a equação do cilindro:

x 2 + y 2 = r 2

Como sempre, só terminamos uma troca depois que verificamos onde cada um desses novos termo ( r ,   θ   e   z ) variam!

Passo 4

Podemos aqui começar pelo caso mais fácil que é a variação do próprio z que sabemos estar variando de uma B a s e até um T e t o :

P l a n o   v e r d e ≤ z ≤ C o n e   a z u l

0 ≤ z ≤ x 2 + y 2

Sim, estamos em outras coordenadas agora, então

0 ≤ z ≤ r 2

0 ≤ z ≤ r

Em relação ao r e ao θ , bem... Siga-me!

Passo 5

Note, você, que o ângulo θ sempre gira no plano x y saindo do eixo x positivo, porém, se repararmos o sólido novamente

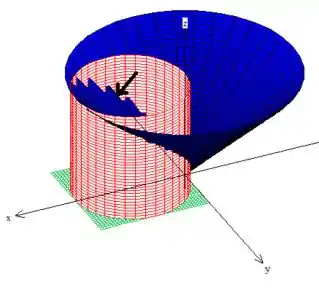
temos que esse ângulo tem que estar dando uma meia volta, mas começando 90 ° atrasado

- π 2 ≤ θ ≤ π 2

Enquanto que o r está indo do 0 até o cilindro

0 ≤ r ≤ c i l i n d r o   v e r m e l h o

O cilindro tem essa equação aqui

x 2 + y 2 = 2 x                       ⇒ S u b s t i t u i n d o a s   p o l a r e s                         r 2 = 2   r cos ⁡ θ     ⇒

r = 2 cos ⁡ θ

Logo

0 ≤ r ≤ 2 cos ⁡ θ

Sacou?

Passo 6

Bem, agora é só montar a integral tripla e correr para o abraço!

∭ W   ρ ( x ,   y , z )   d V = ∭ W     x 2 + y 2 d V

Lembre-se de substituir pelas coordenadas cilíndricas e não deixar de multiplicar pelo J a c o b i a n o ;)

∫ - π 2 π 2 ∫ 0 2 cos ⁡ θ ∫ 0 r r 2   J   d z d r d θ =

∫ - π 2 π 2 ∫ 0 2 cos ⁡ θ ∫ 0 r r 3     d z d r d θ

Resolvendo a integral de dentro considerando r 3 como uma constante...

∫ - π 2 π 2 ∫ 0 2 cos ⁡ θ r 3 ∫ 0 r     d z d r d θ =

∫ - π 2 π 2 ∫ 0 2 cos ⁡ θ r 3 z 0 r d r d θ =

∫ - π 2 π 2 ∫ 0 2 cos ⁡ θ r 4 d r d θ =

Integrando a do meio agora...

∫ - π 2 π 2 ∫ 0 2 cos ⁡ θ r 4 d r d θ =

∫ - π 2 π 2 r 5 5 0 2 cos ⁡ θ d θ =

∫ - π 2 π 2 2 cos ⁡ θ 5 5 d θ = 32 5 ∫ - π 2 π 2 cos 5 ⁡ θ d θ =

Eu sei e te entendo! Essa integral é muito chata, mas não desista! Você está perto! Vamos lá

Esse cosseno aí, podemos separá-lo

32 5 ∫ - π 2 π 2 cos 4 ⁡ θ cos ⁡ θ d θ = 32 5 ∫ - π 2 π 2 cos 2 ⁡ θ 2 cos ⁡ θ d θ =

cosseno ao quadro, sabemos que é, cos 2 ⁡ θ = 1 - sin 2 ⁡ θ

32 5 ∫ - π 2 π 2 1 - sin 2 ⁡ θ 2 cos ⁡ θ d θ = 32 5 ∫ - π 2 π 2 1 - 2 sin 2 ⁡ θ + sin 4 ⁡ θ cos ⁡ θ d θ =

Pow! Repare que podemos agora realizar uma mudança simples...

sin ⁡ θ = t                 →                   d t = cos ⁡ θ d θ

nâo se esqueça de trocar as variações de θ também!

θ = - π 2         ��         →                 sin ⁡ - π 2 = t                 →                         t = - 1

θ = π 2               ��     →                   sin ⁡ π 2 = t                 →                       ��   t = 1

Substituindo tudo...

32 5 ∫ - π 2 π 2 1 - 2 sin 2 ⁡ θ + sin 4 ⁡ θ cos ⁡ θ d θ = 32 5 ∫ - 1 1 1 - 2 t 2 + t 4 d t =

32 5 t - 2 t 3 3 + t 5 5 - 1 1 =

32 5 1 - 2 3 + 1 5 - - 1 + 2 3 - 1 5 = 32 5 2 1 - 2 3 + 1 5 =

Concluímos que

512 75

Resposta

512 75