Seja o sólido limitado por e pelo plano . Calcule
Passo 1
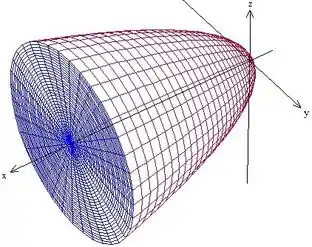
Antes de tudo, vamos fazer um esboço da nossa região, para entendermos melhor o que está sendo pedido. Vemos que é a equação de um paraboloide, mas com simetria em x. O outro cara é um plano . Portanto, temos a seguinte região
Passo 2
Como a região é limitada por um paraboloide e um plano e a função a ser integrada não pede nenhuma mudança específica, vamos usar a mudança cilíndrica.
Passo 3
Precisamos escrever, matematicamente, a nossa região.
Lembre-se que as variáveis normalmente vão ser descobertas da interseção entre os caras envolvidos, ou seja, precisamos achar a interseção do plano com o paraboloide. Como fazemos isso? Igualando as expressões.
Portanto, vão variar dentro desse círculo, ou seja, e .
Precisamos agora determinar a variação de Veja na figura que ele varia da equação do paraboloide até a equação do plano, ou seja
Portanto, nossa região descrita matematicamente será
Passo 4
Vamos agora (finalmente) fazer a substituição esférica na integral:
Passo 5
Vamos realizar a integração em
Passo 6
Realizando a integração em