Responde Aí
Acesse com GoogleAcesse com AppleAcesse com Facebook

Exercícios Resolvidos de Alterações na Mudança de Variável

Ver Teoria
Exercício 1712345678910111213141516181920

Enunciado

Calcule a integral ∭ S z d x d y d z , onde

S = x , y , z ∈   R 3 ; z ≥ 0 ,   2 y ≥ z 2 , z 2 ≥ 4 x 2 + y 2 .

Passo 1

Vamos começar a resolução do nosso problema entendendo melhor sobre o nosso sólido s .

Esse sólido, está dentro de uma superfície, bem peculiar: O cone de equação z 2 = 4 x 2 + y 2 . Note que eu disse que o sólido está dentro! Isso acontece porque o problema nos pediu z 2 ≥ , bele?

S , assim como delimitada pelo cone, também está dentro de um cilindro parabólico de equação 2 y = z 2 e acima do nosso plano z = 0 , ou o plano X Y se preferir.

Se a gente desenhar essas três superfícies juntas

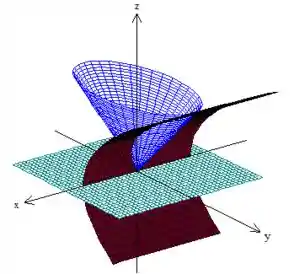
Ganhamos nosso S que está acima desse pedacinho de cone azul e abaixo do cilindro parabólico vermelho. :)

Passo 2

Bem, um bizu para quando temos que resolver uma integral tripla dentro de superfícies como cones e cilindros, é justamente tentar fazer uma substituição para coordenas cilíndricas.

Vamos usar então essa mudança daqui

x = r 2 cos ⁡ θ

y = r sin ⁡ θ

z = z

Note que se a gente substituir na equação do cone, a gente ganha...

z 2 = 4 x 2 + y 2 → z 2 = 4 r 2 cos ⁡ θ 2 + ( r sin ⁡ θ ) 2 →

z 2 = r 2 c o s 2 θ + s i n 2 θ = r 2 →

z = r

Observe como simplificou essa superfície que antes era muita mais complexa!

Justamente por isso que usamos essa mudança, ao invés daquela mudança convencional para coordenadas cilíndricas ( x = r cos ⁡ θ ) , okay?

Passo 3

Pois bem... como toda resolução de integral tripla, temos que descobrir quem são os nossos limites. Vamos começar então pelo nosso z .

A gente pode observar pelo desenho acima que z   está delimitado por baixo pelo pedaço de cone azul e está delimitado por cima pelo pedacinho da superfície vermelha. Ou seja:

c o n e ≤ z ≤ c i l i n d r o   p a r a b ó l i c o

A gente viu no passo anterior que z limitado pelo cone, é o mesmo que falar que z está limitado por r .

Okay! Mas e quanto ao limite superior? Bem, aí teremos...

z 2 = 2 y             ( e q .   d o   c i l i n d r o )

z = 2 y

Repare que só queremos a raiz positiva, pois z ≥ 0 . Agora substituindo as novas variáveis...

z = 2 r sin ⁡ θ

Prontinho! Temos a nossa variação de z

r ≤ z ≤ 2 r sin ⁡ θ

Passo 4

Falta pra gente, ainda, os limites de r e θ que a gente vai encontrar olhando para a projeção desse sólido no plano X Y .

Olhar pra projeção em X Y , significa aqui encontrar a intercessão do cone com o cilindro parabólico. Veja só:

z 2 = 4 x 2 + y 2 z 2 = 2 y →     2 y = 4 x 2 + y 2

Se a gente passar esse termo 2 y para o outro lado e completar quadrado vamos poder enxergar essa curva melhor, concorda?

0 = 4 x 2 + y 2 - 2 y   →   4 x 2 + y - 1 2 - 1 = 0     →   4 x 2 + y - 1 2 = 1    

Opa! Chegamos na equação de uma elipse! Uma elipse deslocada uma unidade para a direita em y e com eixo maior sobre y mesmo

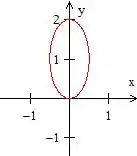
se você se lembrar, o ângulo θ é medido a partir do eixo x no sentido anti-horário, logo, para toda região ser descrita, o θ deve variar de

0 ≤ θ ≤ π

Quanto a variação do raio, bem... ele está em cima da elipse, logo, substituindo as polares na equação da elipse...

2 y = 4 x 2 + y 2   → 2 r sin ⁡ θ = r 2 →

r = 2 sin ⁡ θ

Como o menor valor de r é a origem, concluímos que

0 ≤ r ≤ 2 sin ⁡ θ

Passo 5

Como toda mudança de coordenadas, vamos precisar de multiplicar a função pelo jacobiano, e quem é mesmo o jacobiano?

Um bizu para encontrar o jacobiano em caso de mudança para coordenadas cilíndricas é multiplicar as constantes de x = r 2 cos ⁡ θ   e y = r sin ⁡ θ nas novas coordenadas por r

Dessa forma

J = 1 2   .   1   .   r = r 2

A nossa função em coordenadas polares será

z   .   J = z r 2

Passo 6

Agora é só junta tudo e integrar:)

∭ S z d x d y d z = ∭ S r , θ , z z r 2 d r d θ d z = ∫ 0 π ∫ 0 2 sin ⁡ θ ∫ r 2 r sin ⁡ θ z r 2   d z d r d θ

Resolvendo primeiro a integral de dentro, teremos

∫ 0 π ∫ 0 2 sin ⁡ θ ∫ r 2 r sin ⁡ θ z r 2   d z d r d θ = 1 2 ∫ 0 π ∫ 0 2   s i n θ r z 2 2 r 2 r sin ⁡ θ d r d θ =

= 1 2 ∫ 0 π ∫ 0 2 sin ⁡ θ r r sin ⁡ θ - r 2 2 d r d θ = 1 2 ∫ 0 π ∫ 0 2 sin ⁡ θ r 2 sin ⁡ θ - r 3 2 d r d θ =

Agora resolvendo a integral do meio

1 2 ∫ 0 π ∫ 0 2 sin ⁡ θ r 2 sin ⁡ θ - r 3 2 d r d θ = 1 2 ∫ 0 π sin ⁡ θ r 3 3 0 2 sin ⁡ θ - r 4 2   ∙ 4 0 2 sin ⁡ θ d θ =

= 1 2 ∫ 0 π sin ⁡ θ 2 sin ⁡ θ 3 3 - 2 sin ⁡ θ 4 8 d θ = 1 2 ∫ 0 π s i n 4 θ 8 3 - 6 3 d θ = 1 3 ∫ 0 π s i n 4 θ d θ

Por fim, resolvendo a integral de fora lembrando que s i n 2 θ = 1 - cos ⁡ 2 θ 2 e c o s 2 θ = 1 + cos ⁡ 2 θ 2

1 3 ∫ 0 π s i n 4 θ d θ = 1 3 �� 0 π 1 - cos ⁡ 2 θ 2 2 d θ = 1 3 ∫ 0 π 1 4 1 - 2 cos ⁡ 2 θ + c o s 2 ( 2 θ ) d θ =

= 1 3 ∫ 0 π 1 4 1 - 2 cos ⁡ 2 θ + 1 + cos ⁡ 4 θ 2 d θ = 1 3 ∫ 0 π 3 8 d θ = π 8

Resposta

∭ S z d x d y d z = π 8