Questão 4: Calcule a integral tripla
Onde é o solido constituído dos pontos tais que e
Passo 1
Então, como estamos atrás de uma integral tripla em cima de um sólido que o enunciado nomeou de , é uma boa prática, para facilitar a visualização inclusive, desenhar esse sólido no espaço, então essa será a nossa primeira tarefa aqui, ok?
Primeiro eu quero que você perceba que estamos dentro de uma esfera. Mas não é uma esfera comum, afinal essa daqui está deslocada, veja...
Completando quadrado em lembrando que ...
Viu só?! Então o sólido está dentro de uma esfera que está desloca duas unidades em e, além disso, ela tem raio ...
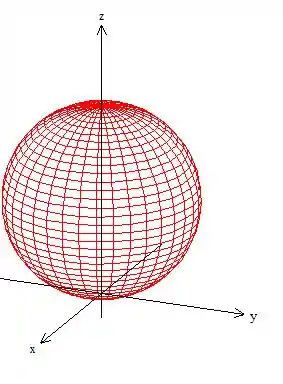
Passo 2
Mas calma aí que ainda não encontramos o nosso sólido ainda não! A outra restrição que o nosso enunciado nos impôs envolve...
Lembrando que a função módulo gera no plano , a seguinte cara...
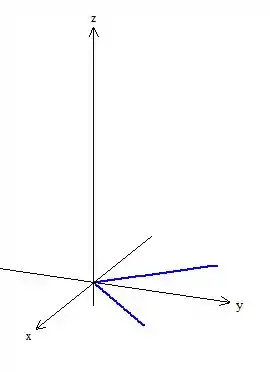
O sinal de menor o igual trata-se dos pontos que estão dentro desse . Ah! E como essa igualdade não depende de , podemos puxar essa tesoura pra cima, assim a gente corta um gomo da nossa esfera:
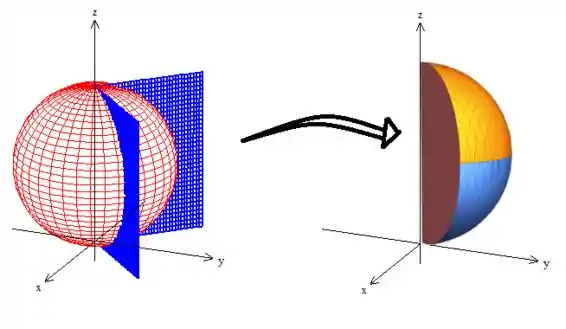
E esse gomo obedece à condição de estar dentro da esfera e ter , logo ele é a nossa superfície !!! ;)
Passo 3
Beleza, agora, com sólido visto, para prosseguirmos com a resolução da integral, podemos começar a tentar descrever esse sólido. E olha que legal, não se trata de um pedaço de uma esfera? Então podemos pensar em uma mudança para coordenadas esféricas com o eixo deslocado:
O Jacobiano dessa mudança, mesmo ela sendo uma mudança para coordenadas esféricas deslocada, continua sendo uma mudança para coordenadas esféricas, portanto Jacobiano não muda e continua sendo:
Passo 4
Agora temos que encontrar a variação das novas variáveis basicamente. Para entender como eles variam, vale a pena inseri-los no desenho:
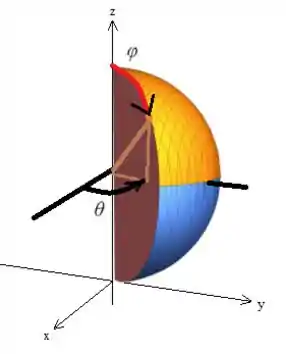
(só tome cuidado, pois só podemos colocar esse eixo de variação das variáveis esféricas, pois fizemos uma mudança adequada pra isso, caso contrário, e não tivesse esse no ali em cima, o eixo de variação estaria na origem, saca?)
Show, com isso podemos tirar que varia de até o raio da esfera que é ...
Quanto ao ângulo , observe que ele vai de até lá em baixo em ...
Já o ângulo , bem esse cara depende da abertura entre o as retas do módulo...
Para ...
E que caso o seno é igual ao cosseno? Justamente! Em . No caso de , vamos obter , onde vemos que...
Passo 5
Podemos finalmente regressar à integral tripla onde devemos substituir tudo (inclusive não se pode esquecer-se de multiplicar pelo Jacobiano)...
Integrando em relação a ...
Integrando em agora...
Cuidado para não substituir os limites em , heim!
Show! :D