Seja o sólido que resulta da interseção das regiões , , , e , calcular o volume de .
Passo 1
Vamos fazer um esboço da região para entender melhor o que está sendo pedido:
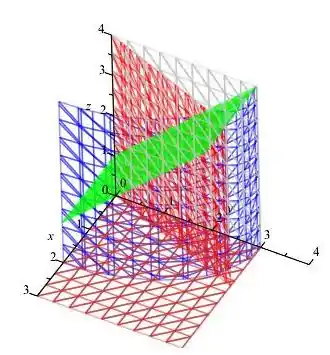
Essa região é um pouco confusa mesmo, vamos por partes.
Temos um cilindro de base elíptica dado por (em azul).
O plano vertical está representado em cinza.
A equação representa no plano uma reta, certo? No ela independe de , então temos essa reta ao longo de , gerando um plano vertical. Como o coeficiente angular é positivo, essa reta corta o e o quadrante. A parte que vai nos interessar é onde , como na figura.
O plano limita a região por baixo, é fácil visualizar. Falta, agora, o plano , representado em verde. Podemos interpretá-lo como a reta do plano repetida ao longo de eixo .
Essa é a região vista de cima, para você entender melhor:
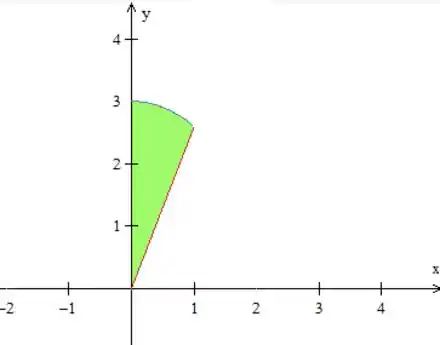
Passo 2
Agora precisamos escrever matematicamente essa região . Como o sólido possui simetria em relação ao eixo e é limitado lateralmente por um cilindro, vamos usar coordenadas cilíndricas. Faremos:
Perceba que o cilindro possui base elíptica! Por isso adicionamos esses coeficientes e na substituição.
Passo 3
Vamos, agora, descobrir os intervalos de integração. Vamos começar pela variação de .
Assim, temos que a variação de será
Passo 4
Pelo gráfico, vemos que os valores de variam desde o plano até o plano , o que nos dá , certo? Vamos, então, fazer a substituição cilíndrica na equação desse plano pra descobrir o outro valor desse :
Temos, então, .
Passo 5
Agora só falta o intervalo de . Veja que o sólido está limitado embaixo pelo plano e em cima pelo plano inclinado (por isso é muito importante que você entenda a região de integração). Vamos, então, fazer a mudança de variáveis nesse plano:
Temos, então . Assim, nossa região de integração será escrita como:
Passo 6
Vamos agora substituir os intervalos que encontramos na integral iterada:
Passo 7
Integrando em relação a , temos:
Passo 8
Agora, integramos em relação a :
Passo 9
Finamente, integramos em relação a :