Calcule a massa da região com função densidade .
Passo 1
O problema pede que calculemos a massa do sólido delimitado pelas superfícies acima, sabendo que sua densidade é dada por . Nós sabemos que:
Onde é o diferencial de massa e o de volume. Integrando ambos os lados na região em que o sólido está contido, temos que:
Passo 2
Antes de tudo, vamos fazer um esboço da região para entender melhor o que está sendo pedido. Temos uma esfera de raio centrada em :
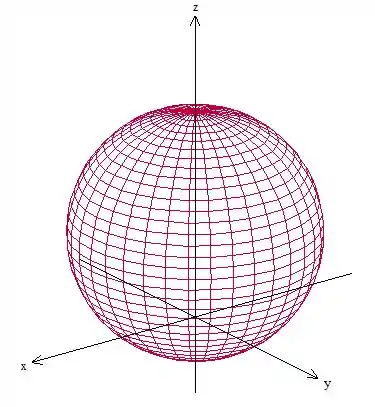
A região do problema é o que está dentro da esfera, beleza?
Passo 3
Como a região é limitada por uma esfera, vamos utilizar coordenadas esféricas:
Na verdade, para facilitar um pouco a vida, vamos usar coordenadas esféricas deslocadas, ok?
Assim, o centro das coordenadas é o centro da esfera, isso vai nos ajudar bastante.
Passo 4
Precisamos escrever matematicamente a região de integração. Como nós deslocamos as coordenadas para o centro da esfera, ela passa a ser escrita como , no caso:
Você pode verificar isso fazendo a mudança esférica na sua equação!
O termo da equação vai ser cancelado pelo da mudança esférica.
Bom, como se trata da esfera inteira, , o que nos dá:
Passo 5
Vamos agora fazer a substituição esférica na integral:
Passo 6
Agora vamos integrar em relação a :
Passo 7
Agora em relação a :
Passo 8
Agora vamos integrar em relação a :