- Calcule a massa do sólido limitado superiormente por , inferiormente por sendo a densidade igual ao quadrado da distância de ao plano .
Passo 1
Cara, massa de um sólido a essa altura do campeonato para a gente não é nada mais é do que uma integral tripla
Onde é a função de densidade do sólido.
Mas aí surge duas duvidas não é verdade?!
- Quem é o sólido que estamos trabalhando?
- Quem é a função ?
Passo 2
Vamos começar aqui respondendo a primeira pergunta!
Pow, para entender esse sólido profundamente, você deve já ter em mente que essa equação aqui representa uma esfera, mas não é uma esfera qualquer, e sim uma deslocada uma unidade para cima:
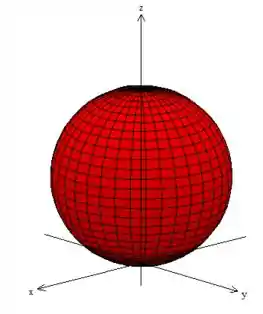
Enquanto isso, representa um cone:
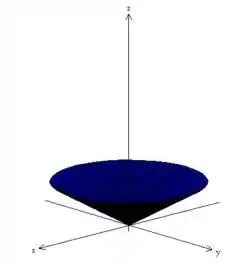
Bem, se você quer entender o sólido, desenhe essas superfícies delimitadoras juntas no espaço. Obtendo sorvete aqui, oh:
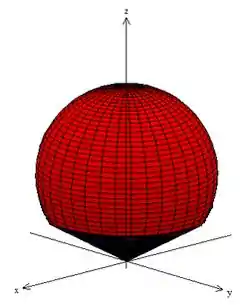
Passo 3
Bem, estamos trabalhando dentro de uma esfera, então... Nada mais justo utilizarmos as coordenadas esféricas, onde
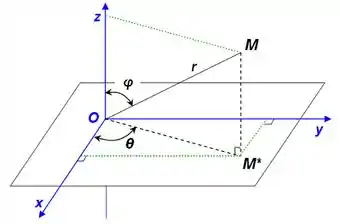
O jacobiano dessa mudança é
Nunca devemos sair de uma mudança enquanto não encontramos onde essas novas variáveis estão variando. Bora?
Passo 4
Vamos primeiro ver os ângulos e como eles variam, beleza? Bem, o primeiro ângulo a gente tira de letra se lembrarmos que nosso sólido nada mais é do que um sorvetão que da uma volta completa em torno do eixo . Sendo assim:
Agora o outro ângulo vai ser um pouco mais complicadinho de ver. Vamos tentar ver como a parte da “casquinha” do sorvetão se comporta no plano ZY? Bora lá:
Graficamente, temos:
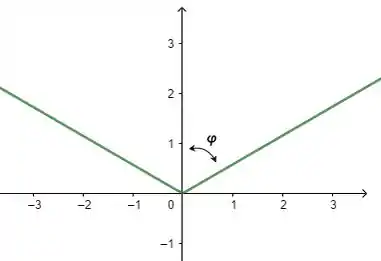
Ok, mas pra que isso? Repare que fazendo isso fica evidente quem vai ser o ângulo !
Show de bola, outro ângulo foi encontrado!
Mas e o nosso querido , quem vai ser? Se olharmos de novo pro sorvetão e pra própria definição do vamos notar que o sai da origem e toca no topo do sólido, isso é, na parte da própria bola de sorvete. E quem é a bola de sorvete se não a própria esfera? Vamos primeiro reescrever a equação da esfera:
Beleeeza, agora o pulo do gato vai ser substituir as coordenadas polares na última equação acima pra ver o que encontramos:
E como , assim como , vamos ter:
Ufa, algumas linhas depois a gente achou o nosso . Sendo assim, vamos ficar com:
Passo 5
Opa, perai, faltou alguém não? E a função densidade? O enunciado é meio enrolado, mas como ele disse “a densidade igual ao quadrado da distância de ao plano .”, vamos ter simplesmente que:
E, passando pras coordenadas polares:
Passo 6
Eu sei que você queria que tivesse acabado, mas como dizia minha avó: “calma que falta menos que faltava”. O que sobrou foi só o trabalho braçal. Vamo que vamo então:
Aplicando as coordenadas polares
Agora é só tacar tudo que a gente descobriu dentro do liquidificador:
Resolvendo primeiro em função de :
Resolvendo agora em função de :
E por fim, em função de :
Voltando para a variável original e aplicando os limites de integração originais:
Resposta
![]()