Responde Aí
Acesse com GoogleAcesse com AppleAcesse com Facebook

Exercícios Resolvidos de Alterações na Mudança de Variável

Ver Teoria
Exercício 1612345678910111213141517181920

Enunciado

Questão dois: calcule o volume do sólido interior à esfera x 2 + y 2 + z 2 = 1 e exterior aos cones z 2 = x 2 + y 2 e x 2 = 3 y 2 + z 2 .

Passo 1

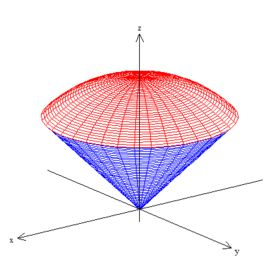
Pow, antes de procurarmos o volume desse cara aí, vamos tentar enxergar esse sólido um pouco desenhando no espaço às três superfícies do enunciado:

x 2 + y 2 + z 2 = 1 é uma esfera de raio 1 :

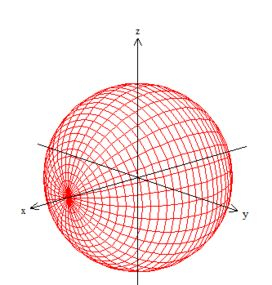
que está delimitada por esse cone z 2 = x 2 + y 2 ao redor de z ...

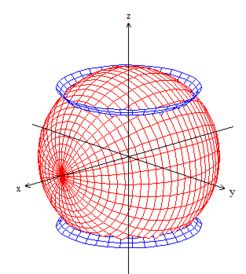
e também por esse outro cone x 2 = 3 y 2 + z 2 ao redor de x :

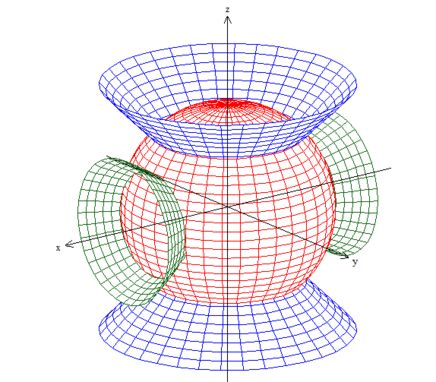
Viu, só? O sólido que queremos está no interior a essa esfera, mas pra fora dos dois cones!

Passo 2

Bem, para encontrar esse volume pedido V p , pegamos o volume total da esfera V e subtraímos pelo volume que esse cone z 2 = x 2 + y 2 ocupa na esfera, V 1 , e também o que esse x 2 = 3 y 2 + z 2 abrange, V 2 :

V p = V - V 1 - V 2

O volume V da esfera é tranquilo pra gente:

V = 4 3 π R 3         →          

afinal sabemos que o seu raio é R = 1 ...

V = 4 3 π

Já os dois volumes que estão dentro dos cones e delimitado pela esfera, não é tão simples assim, e teremos de usar uma integral tripla pra isso, afinal, sabemos que um volume pode ser encontrado:

V o l u m e = ∭ W   1 d V

Passo 3

Vamos começar aqui calculando o volume que está dentro desse primeiro cone V 1 , z 2 = x 2 + y 2 , aqui:

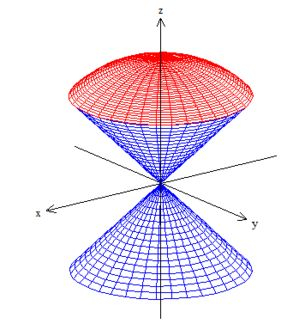
Como vimos o seu cálculo será feito utilizando uma integral tripla:

V 1 = ∭ W   1 d V

O W no caso é esses sorvetes aí, como tem dois do mesmo jeito, vamos pegar apenas o sorvete de cima que vamos chamar de W c :

V 1 = 2 ∭ W c   1   d V

Muito bem, como estamos dentro de uma esfera... Nada mais justo que utilizarmos as coordenadas esféricas,

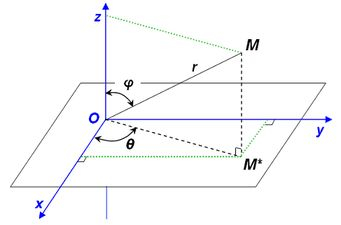
onde vamos trocar

x = r sin ⁡ φ cos ⁡ θ

y = r sin ⁡ φ sin ⁡ θ

z = r cos ⁡ φ                  

O jacobiano dessa mudança é

J = r 2 sin ⁡ φ

Nunca devemos sair de uma mudança enquanto não encontramos onde essas novas variáveis estão variando. Bora?

Passo 4

Vamos começar aqui falando do mais fácil, o raio! Bem, ele está variando da origem até o raio limite que é o da própria esfera:

0 ≤ r ≤ R a i o   d a   e s f e r a

0 ≤ r ≤ 1

Esse ângulo θ também é bem fácil, basta você observar que a esfera dá uma volta completa ao redor do eixo z , logo

0 ≤ θ ≤ 2 π

Quanto ao ângulo φ , bem... Ele é um pouquinho mais chato, mas não se preocupe que você vai pegar fácil também, vêm comigo separado

Passo 5

Bem, se você reparar novamente no sólido,

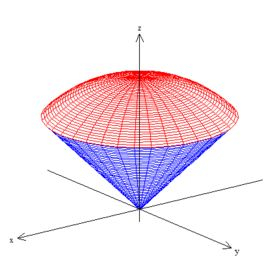
você vai notar que o ângulo φ está variando do eixo z até o cone azul:

0 ≤ φ ≤ C o n e   a z u l

O cone azul tem equação z 2 = x 2 + y 2 . Epa! Estamos trabalhando com as coordenadas cilíndricas, então devemos substitui-las nessa equação:

z 2 = x 2 + y 2                   →                           r cos ⁡ φ 2 = r sin ⁡ φ cos ⁡ θ 2 + r sin ⁡ φ sin ⁡ θ 2                     →

      r cos ⁡ φ = r 2 sin 2 ⁡ φ cos 2 ⁡ θ + r 2 sin 2 ⁡ φ sin 2 ⁡ θ                         →

    r cos ⁡ φ = r 2 sin 2 ⁡ φ cos 2 ⁡ θ + sin 2 ⁡ θ = r 2 sin 2 ⁡ φ

Como o seno é positivo e o raio também...

r cos ⁡ φ = r sin ⁡ φ     →         1 ∙   r cos ⁡ φ = r sin ⁡ φ

passando esse r cos  ⁡ φ pro outro lado dividindo...

r sin ⁡ φ r cos ⁡ φ = 1           →           tan ⁡ φ = 1

Nessas condições, φ = 45 ° = π 4

Logo

0 ≤ φ ≤ π 4

Passo 6

Então podemos voltar a integral que estamos trabalhando aqui:

V 1 = 2 ∭ W c   1   d V

e substituindo tudo que encontramos não esquecendo de multiplicar o 1 ali pelo Jacobiano:

V 1 = 2 ∫ 0 2 π ∫ 0 π 4 ∫ 0 1 J d r d φ d θ =

2 ∫ 0 2 π ∫ 0 π 4 ∫ 0 1 r 2 sin ⁡ φ d r d φ d θ =

Integrando a de dentro:

2 ∫ 0 2 π ∫ 0 π 4 sin ⁡ φ ∫ 0 1 r 2 d r d φ d θ =

2 ∫ 0 2 π ∫ 0 π 4 sin ⁡ φ r 3 3 0 1 d φ d θ =

2 3 ∫ 0 2 π ∫ 0 π 4 sin ⁡ φ d φ d θ =

Integrando a do meio:

2 3 ∫ 0 2 π ∫ 0 π 4 sin ⁡ φ d φ d θ =

2 3 ∫ 0 2 π - cos ⁡ φ 0 π 4 d θ =

2 3 ∫ 0 2 π - cos ⁡ π 4 - - cos ⁡ 0 d θ =

2 3 ∫ 0 2 π - 2 2 - - 1 d θ =

2 3 1 - 2 2 ∫ 0 2 π d θ =

Calculando a última integral:

2 3 1 - 2 2 2 π =

4 π 3 1 - 2 2

Esse é o volumo de dentro desses cones certinho V 1 !

Passo 7

Mas, sim, não acabamos, pois ainda falta o volume dentro do cone deitadinho em x , o V 2 ...

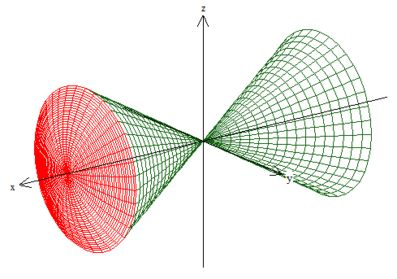
A boa notícia é que ele é bem semelhante ao anterior, logo vamos pegar novamente, apenas o dobro do sorvete deitadinho pra direita ( W 2 )

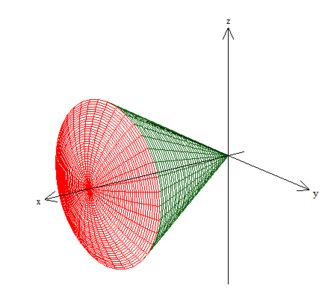
e falar que:

V 2 = 2 ∭ W 2   1   d V

Usando novamente as coordenadas esféricas

x = r sin ⁡ φ cos ⁡ θ

y = r sin ⁡ φ sin ⁡ θ

z = r cos ⁡ φ                  

J = r 2 sin ⁡ φ

porém, como estamos ao redor de x e não de z , basta trocar as variáveis x por z :

z = r sin ⁡ φ cos ⁡ θ

y = r sin ⁡ φ sin ⁡ θ

x = r cos ⁡ φ                  

O jacobiano dessa mudança é

J = r 2 sin ⁡ φ

Sacou?

Então vamos aos limites das novas variáveis!

Passo 8

O raio novamente sai da origem até o raio máximo que é a esfera vermelha:

0 ≤ r ≤ 1

e θ , dessa vez no plano z y (pois, agora o z e o y que tem θ )

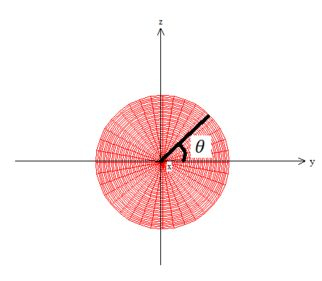
E ele também...

0 ≤ θ ≤ 2 π

Quanto ao ângulo φ , dessa vez sando do eixo x (pois é o x que tem φ : x = r cos ⁡ φ ):

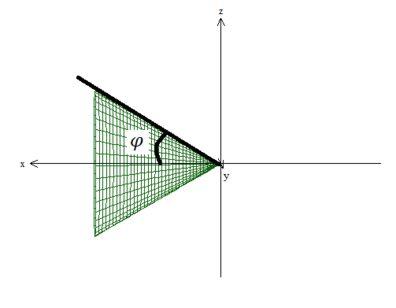
basta substituir essas coordenadas na equação desse cone:

x 2 = 3 z 2 + y 2                   →                           r cos ⁡ φ 2 = 3 r sin ⁡ φ cos ⁡ θ 2 + r sin ⁡ φ sin ⁡ θ 2                     →

      r cos ⁡ φ = 3 r 2 sin 2 ⁡ φ cos 2 ⁡ θ + r 2 sin 2 ⁡ φ sin 2 ⁡ θ                         →

    r cos ⁡ φ = 3 r 2 sin 2 ⁡ φ cos 2 ⁡ θ + sin 2 ⁡ θ = 3 r 2 sin 2 ⁡ φ

Como o seno é positivo e o raio também...

r cos ⁡ φ = 3   r sin ⁡ φ     →         1 ∙   r cos ⁡ φ = r sin ⁡ φ

passando esse r cos  ⁡ φ pro outro lado dividindo...

r sin ⁡ φ r cos ⁡ φ = 1 3           →           tan ⁡ φ = 3 3

Nessas condições, φ = 30 ° = π 6

Logo

0 ≤ φ ≤ π 6

Passo 9

Então podemos voltar a integral que estamos trabalhando aqui:

V 2 = 2 ∭ W 2   1   d V

e substituindo tudo que encontramos não esquecendo de multiplicar o 1 ali pelo Jacobiano:

V 2 = 2 ∫ 0 2 π ∫ 0 π 6 ∫ 0 1 J d r d φ d θ =

2 ∫ 0 2 π ∫ 0 π 6 ∫ 0 1 r 2 sin ⁡ φ d r d φ d θ

Uma integral realmente muito parecida, viu?!

Integrando a de dentro:

2 ∫ 0 2 π ∫ 0 π 6 sin ⁡ φ ∫ 0 1 r 2 d r d φ d θ =

2 ∫ 0 2 π ∫ 0 π 6 sin ⁡ φ r 3 3 0 1 d φ d θ =

2 3 ∫ 0 2 π ∫ 0 π 6 sin ⁡ φ d φ d θ =

Integrando a do meio:

2 3 ∫ 0 2 π ∫ 0 π 6 sin ⁡ φ d φ d θ =

2 3 ∫ 0 2 π - cos ⁡ φ 0 π 6 d θ =

2 3 ∫ 0 2 π - cos ⁡ π 6 - - cos ⁡ 0 d θ =

2 3 ∫ 0 2 π - 3 2 - - 1 d θ =

2 3 1 - 3 2 ∫ 0 2 π d θ =

Calculando a última integral:

2 3 1 - 3 2 2 π =

4 π 3 1 - 3 2

Esse é o volumo de dentro desses cones certinho V 2 !

Passo 10

Finalmente retornando ao que queríamos desde o começo lá no passo 2 , ou seja, o volume pedido V p ...

V p = V - V 1 - V 2

V p = 4 3 π - 4 π 3 1 - 2 2 - 4 π 3 1 - 3 2 =

V p = 4 3 π - 4 π 3 + 4 π 3 2 2 - 4 π 3 + 4 π 3 3 2 =

V p = 4 π 2 6 - 1 3 + 3 6

Resposta

4 π 2 6 - 1 3 + 3 6