Calcule onde é a região do limitada por e .
Passo 1
Vamos fazer um esboço da região para entender melhor o que está sendo pedido. Temos um paraboloide de seção elíptica com simetria no eixo cortado pelo plano :
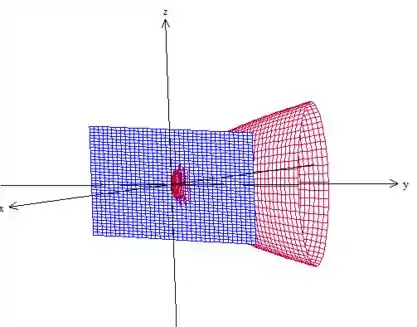
Nossa região é essa parte do paraboloide cortada pelo plano, essa casca que está à frente do plano. Podemos ver de outro ângulo para visualizar melhor:
Passo 2
Vamos agora escrever matematicamente essa região. Podemos fazer o seguinte: dizer que a variável está entre o plano azul e o paraboloide e definir a projeção do sólido no plano , que, no caso, vai ser uma elipse. Vamos nos preocupar com essa projeção em mais tarde, por enquanto, dizemos que essa região é .
Isso nos dá:
Passo 3
Agora vamos calcular isso aí:
Ok, agora precisamos escrever essa região . Nós sabemos que ela é a projeção no plano do sólido dado pela interseção do paraboloide com o plano , então, antes de mais nada, vamos fazer a interseção dessas duas equações:
Rearrumando isso aqui:
Tá, que porcaria é essa? Calma, vamos por partes. Sabemos que é uma circunferência no plano centrada na origem né? Se tivermos é uma elipse centrada na origem.
Agora, com esse termo , deslocamos essa elipse da origem, na direção . Beleza, então a projeção do sólido no plano é uma elipse deslocada da origem.
Como é uma elipse, a boa é usar coordenadas elípticas. Como temos um coeficiente ali no , vamos levar o coeficiente para a coordenada :
E vamos fazer o seguinte, vamos “levar” o centro dessas coordendas para o centro da elipse de uma vez:
Lembrando que o coeficiente vai para o Jacobiano.
Mas por que fizemos tudo isso na mudança de coordenadas? Porque substituindo essas coordenadas na equação da elipse, encontramos:
Olha que lindo, nessas coordenadas é como se a elipse deslocada tivesse “virado” uma circunferência de raio centrada na origem bonitinha.
Então, para descrever ela temos e . Fazendo a mudança de variáveis na integral, temos:
Passo 4
Agora vamos resolver essa integral dupla:
Agora precisamos usar a seguinte identidade: