Coordenadas cilíndricas
Calcule o volume do sólido limitado pela superfície de equação
E os planos e .
Passo 1
Vamos começar fazendo um esboço disso aí. Temos um hiperboloide de uma folha com simetria em (a variável que tem sinal diferente) cortado por dois planos:
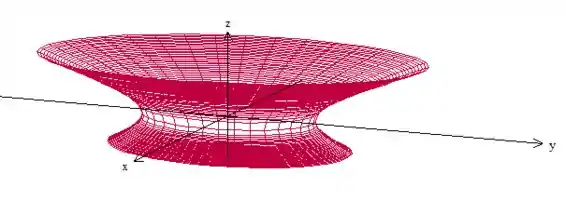
O hiperboloide tem seção elíptica, porque e tem coeficientes diferentes.
Então, é a região dentro do hiperboloide e entre os planos e . Seu volume é dado por
Passo 2
Como a região tem simetria em relação ao eixo , vamos usar coordenadas cilíndricas com os coeficientes do hiperboloide:
Fazendo a mudança, temos:
Como o raio vai desde até o hiperboloide, temos .
Como o enunciado já diz, . Sabemos que porque temos uma volta completa em torno de .
Passo 3
Temos então
Agora é só resolver isso aí: