Calcule a integral tripla
Onde é o sólido, no primeiro octante, resultado da interseção de , , e .
Passo 1
Vamos começar entendendo um pouco mais sobre quem é o nosso sólido D.
A gente já sabe que nos representa no plano cartesiano uma elipse centrada na origem. Porém, no espaço tridimensional ela representa um cilindro de base elíptica e centrado no eixo pois a função independe dessa variável
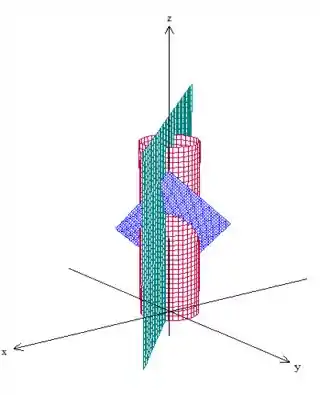
O nosso sólido também está delimitado na lateral pelo plano que reparte o nosso cilindro na vertical como podemos ver representado pelo plano verde.
E por fim, mas não menos importante, o nosso sólido está localizado abaixo do nosso plano em azul, mas acima do plano pois queremos apenas o primeiro octante!
Passo 2
Como estamos integrando dentro de um cilindro, é conveniente para gente utilizar a mudança para coordenadas cilíndricas:
Perceba que utilizamos ao invés da tradicional mudança . Fizemos isso, pois o nosso cilindro é formado por uma elipse, logo
A gente observa então que com essa mudança, o nosso varia de ao raio máximo que , ou seja
Passo 3
Ainda falta encontrar os limites de e de . Bora lá?!
Para a gente entender os limites de , vamos olhar para a projeção do nosso sólido no plano
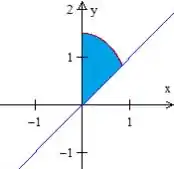
Observamos que está variando acima da reta , e isso acontece devido a condição inicial de . Logo:
Passando para o outro lado dividindo, teremos
Concluímos que o mínimo é o arco . Como a região está limitada no primeiro octante, temos
Vamos encontrar o limite agora?
Então, está limitado inferiormente pelo plano e superiormente pelo plano
Logo
Passo 4
Como as nossas mudanças de coordenas cilíndricas não são as que estamos acostumados, devemos procurar agora o nosso Jacobiano
Passo 5
O nosso próximo passo é justamente eliminar as coordenas cartesianas da nossa função de integração
Mas lembre-se de que quando fazemos uma mudança de coordenadas, não podemos esquecer de multiplicar a nossa nova função pelo nosso Jacobiano. Assim:
Passo 6
Prontinho! Basta montarmos nossa integral e correr para o abraço! :)
Resolvendo a nossa integral, começando pela integral de dentro, vamos obter
Substituindo os limites de integração em , obteremos
Substituindo os limites acima obteremos