Obtenha os vértices e do triângulo equilátero , sendo e sabendo que o lado está contido na reta de equação vetorial .
Passo 1
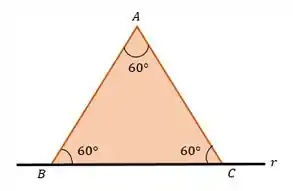
O enunciado nos pede para descobrirmos as coordenadas dos pontos e . Para isso ele nos dá algumas informações!! Diz que e são vértices de um triângulo equilátero, ou seja, os Ângulos são de . Dá que o ponto possui coordenadas. Além disso, fala que os ponto e pertencem à reta que possui equação vetorial . Então, podemos montar a seguinte figura:
Passo 2
Vimos na teoria como encontrar o ângulo entre duas retas, certo? Então, vamos utilizar isso a nosso favor!! Mas, como?
Bem, o ângulo entre a reta e a reta que forma o lado dos pontos e sabemos que vale . Além disso, temos o vetor diretor de e conseguimos o vetor diretor da reta que contém e , pois o próprio vetor , é diretor da reta. Assim, descobriremos as coordenadas de .
Mas, antes, tem um detalhe importantíssimo, sem ele não resolvemos o problema!!
Como pertence à reta , então o formato geral de por meio da equação vetorial da reta é:
Vamos começar então!!
Passo 3
A fórmula do ângulo entre retas é:
Então, vamos calcular o módulo do produto interno, os módulos e o :
Substituindo na fórmula temos:
Elevando os dois lado ao quadrado:
Passo 4
Como temos dois valores de ou acabamos descobrindo os dois pontos e :
Assim, os dois pontos são: