UFRJ, P3-2019.1
Seja um paralelogramo com todos os lados de tamanho . As diagonais de possuem tamanhos e , assinale o valor do menor ângulo interno de :
Passo 1
Belezinha galera, se a gente fosse desenhar esse paralelogramo, teríamos mais ou menos isso aqui:
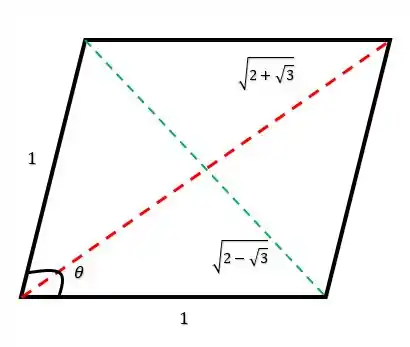
Onde os lados são iguais a , a diagonal maior em vermelho mede , e a diagonal menor em verde mede . O menor ângulo, é aquele formado em . Logo, podemos montar um triângulo com a diagonal menor e os lados de :
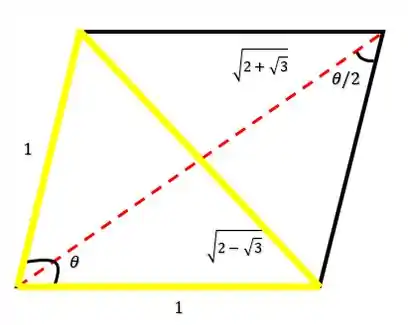
E agora a gente pode aplicar a Lei dos Cossenos nesse triângulo, onde a diagonal menor é o lado oposto ao ângulo , então:
Logo, nosso ângulo vale Resposta certa, letra (d).
Resposta
Letra (d).
Exercícios de Livros Relacionados
Disputando uma partida de sinuca com seus amigos, Paulinho viu-se diante da situação ilustrada na Figura 19-3 (a), em que o ponto B representa a bola branca, P ,a preta, e R a rosa (esta era a bola da
Determinar o ângulo que a reta que passa por A = ( 3 , - 1,4 ) E B = ( 1,3 , 2 ) forma com a sua projeção sobre o plano x y .
Determinar o ângulo entre as seguintes retas:a) r 1 : x = - 2 - t y = t z = 3 - 2 t e r 2 : x 2 = y + 6 1 = z - 1 1 b) r 1 : y = - 2 x + 3 z = x - 2 e r 2 : y = z + 1 - 1 ; x = 4 c) r 1 : x = 1 + 2 t
Determinar o ângulo entre as seguintes retas:a) r 1 : x = - 2 - t y = t z = 3 - 2 t e r 2 : x 2 = y + 6 1 = z - 1 1 b) r 1 : y = - 2 x + 3 z = x - 2 e r 2 : y = z + 1 - 1 ; x = 4 c) r 1 : x = 1 + 2 t
Determinar o valor de n para que seja de 30 ° o ângulo entre as retasa) r 1 : x - 2 4 = y 5 = z 3 e r 2 : y = n x + 5 z = 2 x - 2 b) r 1 : y = n x - 1 z = 2 x e r 2 : eixoO y