Sejam dados os pontos , e . Mostre que , e não são colineares e escreva uma equação vetorial para a reta que contém a altura do triângulo relativa ao vértice .
Passo 1
Se formarmos dois vetores com esses pontos:
Para que os pontos , e sejam colineares, esses vetores deveriam ser paralelos, ou seja, deveria existir um tal que
Da primeira linha temos que , mas da segunda linha temos que , o que é um absurdo né? Logo, não existe que satisfaça esse sistema e portanto os vetores e não são paralelos.
Loogo, os pontos , e não são colineares.
Passo 2
Seja o vetor diretor da reta .
Seja um vetor . Esse vetor, pela regra da mão direita, vai ser perpendicular ao plano em que se encontra o triângulo e consequentemente perpendicular a .
Além disso, como é a altura do triângulo relativa ao vértice , ele vai ser perpendicular à face oposta, ou seja, perpendicular a .
Então, novamente pela regra da mão direita, vai ser paralelo ao vetor resultante de .
Passo 3
Simm, eu sei que ta meio abstrato de entender. Mas olha, vamos encontrar o vetor
Por enquanto temos isso, sendo o vetor preto
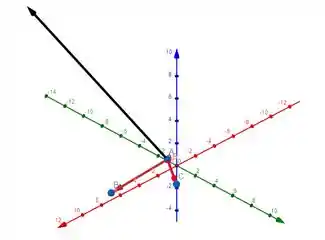
Passo 4
Agora vamos encontrar o vetor
Fazendo o produto vetorial (repare que vamos dividir a segunda linha por 3 para facilitar o cálculo)
Logo, o vetor é paralelo a , que é um vetor diretor da reta .
Na imagem abaixo, é o vetor verde
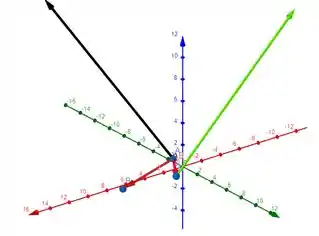
Passo 5
Como a reta passa pelo ponto e tem como vetor diretor, sua equação vetorial vai ser