Um bloco de massa , em repouso numa mesa horizontal sem atrito, é ligado a um suporte rígido por duas molas de constante elástica e . Uma bala de massa e velocidade atinge o bloco como mostrado na figura abaixo.
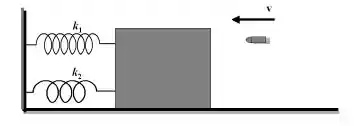
Este sistema de duas molas da figura acima é equivalente a um sistema composto por apenas uma mola cuja constante elástica vale:
- Deduza a expressão .
- A velocidade do bloco imediatamente após a colisão.
Agora, considere e determine em função de , , :
Passo 1
a)
Vamos deduzir partindo da força resultante que as duas molas fazem sobre o bloco:
Sendo:
Logo:
Beleza! Mas será que existe uma relação entre os s?
Bom, como o bloco não tomba nem vai se deslocar torto, o deslocamento de cada mola deve ser igual, lembra? Vamos dar uma olhada na figura:
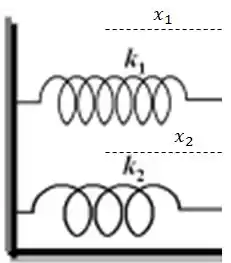
Caso a caixa tombaria pra frente, por exemplo. Logo:
O deslocamento da força resultante também deve ser igual. Isso acontece por que o significado da associação de molas nos diz que as duas molas poderiam ser substituídas por uma única mola cuja constante é a constante resultante.
E qual seria o deslocamento dessa mola? Fica claro que deveria ser o mesmo que o das duas molas, não é?
Logo:
Passo 2
b)
Vamos resolver essa parte usando a conservação de momento do sistema. O momento se conserva já que se trata de uma colisão.(:
Antes da colisão, a bala tinha velocidade e o bloco tinha velocidade nula, logo, o momento inicial é:
Após a colisão, tanto o bloco quanto a bala se deslocam com a mesma velocidade
Como :
E essa é a velocidade do bloco logo após a colisão!
Resposta
a)
Demonstração.
b)