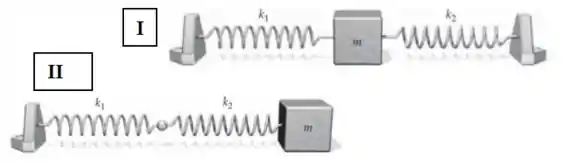
Considere a situação I e II ilustradas nas figuras abaixo. Analise as alternativas abaixo:
i)O bloco de massa m oscila com frequência onde para situação I e para a II.
ii)O bloco de massa m oscila com frequência onde para situação I e para a II.
iii) O bloco de massa m oscila com frequência onde para ambos os sistemas.
iv) Se o bloco de massa oscila com a mesma amplitude para ambos os sistemas teria maior energia mecânica.
v) Se o bloco de massa m oscila com a mesma amplitude para ambos os sistemas, têm mesma energia mecânica.
vi) Se o bloco de massa oscila com a mesma amplitude para ambos os sistemas, não podemos concluir sobre qual sistema teria maior energia mecânica uma vez que isso dependeria dos valores de e .
a)São verdadeiros os itens i, iv
b)São verdadeiros os itens ii, v.
c)São verdadeiros os itens iii, vi
d)Somente o item v é verdadeiro.
e) Somente o item vi é verdadeiro
Passo 1
Opa, temos duas configurações para molas que não são conhecidas pela gente, não é mesmo? Mas vamos ver se conseguimos deduzir como serão as consatntes equivalentes em ambos os casos.
Caso I:
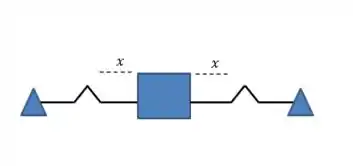
O que acontece nesse caso é o seguinte: Quando o bloquinho se desloca em metros, ele comprime uma mola e estica a outra. O efeito global disso é que as forças serão somadas :
Isso ocorre porque as forças possuem a mesma direção e sentido:
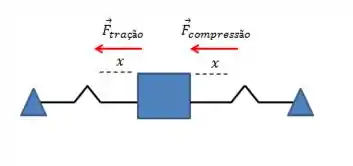
E o que isso quer dizer? Quer dizer que a constante equivalente vale:
Passo 2
Caso 2:
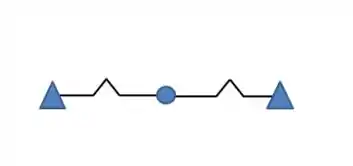
Essa situação não é muito diferente dessa:
Ou seja, uma associação de molas em série. Assim, a constante equivalente é dada por:
Passo 3
E como as molas oscilam? Elas oscilam com um frequência angular dada por:
Assim:
Portanto, analisando as afirmações, concluiremos que estão corretas:
Resposta
a)