Escrever a Tag aqui (nome do capítulo IGUALZINHO), Outra tag, Mais uma tag
Uma plataforma de massa está presa a duas molas ideais sem massa de constantes elásticas e e pode deslizar sobre uma superfície horizontal sem atrito, como indicado na figura.
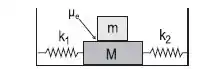
Um bloco de massa é colocado sobre a plataforma. Sendo o coeficiente de atrito estático entre as superfícies do bloco e da plataforma, pode-se afirmar que a amplitude máxima de oscilação do sistema para que o bloco não deslize é:
Passo 1
Vamos primeiro calcular a força elástica que age em
Quando a massa se move na direção , ela sofre uma compressão da mola da direita e é puxada pela mola da esquerda.
Assim, a força elástica fica :
Passo 2
Tanto a massa de baixo quanto a massa de cima sofre a ação dessa força. Então, podemos dizer que a aceleração do conjunto é dado por:
Passo 3
A força de atrito agindo na massa de cima tem que compensar essa aceleração. Assim, podemos dizer que:
A força de atrito é dada pelo produto da normal que age na massa pelo coeficiente de atrito, assim:
Assim:
Passo 4
Fazendo , ou seja, considerando a situação em que há a máxima amplitude de oscilação( e tomando o módulo da expressão):
Assim:
c)
Resposta
c)