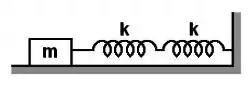
Na figura, duas molas são ligadas e conectadas a um bloco de massa que é posto em oscilação sobre um piso sem atrito. Cada uma das molas possui constante elástica . Qual é a frequência das oscilações?
Passo 1
Primeiramente, vamos descobrir a constante da mola resultante da associação em série das molas da figura. Como elas estão em série, usaremos:
Com
Passo 2
Agora a gente precisa encontrar a frequência de oscilação! Bom, você lembra qual equação relaciona a constante da mola à velocidade angular? Esta aqui:
E a frequência angular pode ser escrita como:
Onde é a frequência de oscilação! Unindo as duas equações:
Substituindo , e calculando, obtemos:
Tranquilo, não é verdade? (: