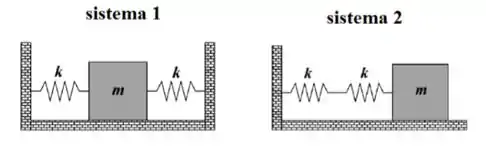
Considere dois sistemas massa-mola contendo duas molas de constante elástica k e um bloco de massa m. A razão entre a frequência natural do sistema 1 e a frequência natural do sistema 2 é:
Passo 1
Vamos olhar primeiro o sistema .
Se deslocarmos o bloco para direita (por exemplo) a mola da direita irá empurrar o bloco com uma força e o bloco da esquerda irá puxar o bloco com uma força também. Assim a força total será
Que funciona como um sistema massa mola com uma constante de mola . Como a frequência é dada por
Passo 2
Agora vamos olhar para o sistema .
Temos que a primeira mola se distende de e a segunda , de forma que o bloco de desloca dado por
No bloco há uma constante de mola efetiva enquanto que em cada mola uma constante de mola .
Como a força sobre cada uma das molas e sobre o bloco é a mesma força , e como , ou melhor, , temos
De forma que a frequência nessa situação será dada por
Passo 3
Assim a razão fica
Resposta
(C)