Identifique se cada afirmação é verdadeira ou falsa. Justifique.
(d) A função definida por é produto interno sobre
Passo 1
A afirmação é falsa.
Pra ser produto interno, uma função deve satisfazer algumas regrinhas, que são os seguintes axiomas:
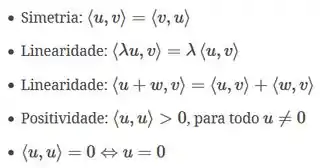
A princípio a gente teria que verificar cada uma dessas propriedades para a função f dada no enunciado.
Se todas elas fossem satisfeitas, então f seria um produto interno.
Mas note que a primeira regrinha já não é satisfeita.
Foi dado que
Mas se a gente trocar a ordem dos vetores, vamos ficar com:
E não necessariamente isso vai ser igual ao que tínhamos antes, pois os valores de , , e são quaisquer.
Logo, f não é um produto interno.
Resposta
Ei, a resposta está no passo a passo :)
Exercícios de Livros Relacionados
Sejam u = x 1 ,y 1 ev = x 2 ,y 2 . Mostrar que cada operação a seguir define um produto interno no I R 2 : u ∙ v = x 1 x 2 + y 1 y 2 u ∙ v = 2 x 1 x 2 + 5 y 1 y 2 u ∙ v = x 1 x 2 + x 1 y 2 + x 2 y 1 +
Sejam os vetores v 1 = x 1 , y 1 ev 2 = x 2 , y 2 de V = R 2 . Verificar quais das funções f : V× V → R , definidas abaixo, são produtos internos em V .g) f v 1 , v 2 = 4 x 1 x 2 + x 1 y 2 + x 2 y 1 +
Sejam os vetores v 1 = x 1 , y 1 ev 2 = x 2 , y 2 de V = R 2 . Verificar quais das funções f : V× V → R , definidas abaixo, são produtos internos em V .e) f v 1 , v 2 = x 1 x 2 + y 1 y 2 + 1
Sejam os vetores v 1 = x 1 , y 1 ev 2 = x 2 , y 2 de V = R 2 . Verificar quais das funções f : V× V → R , definidas abaixo, são produtos internos em V .c) f v 1 , v 2 = x 1 2 x 2 + y 1 y 2 2
Sejam os vetores v 1 = x 1 , y 1 ev 2 = x 2 , y 2 de V = R 2 . Verificar quais das funções f : V× V → R , definidas abaixo, são produtos internos em V . f v 1 , v 2 = 2 x 1 x 2 + 3 y 1 y 2