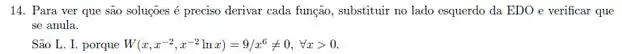Passo 1
Vamos primeiro verificar se as funções são soluções da nossa EDO. Para isso precisamos encontrar suas derivadas e substituir na expressão.
Substituindo
Então a função é solução da EDO. Vamos fazer o mesmo para as outras.
A função é solução da EDO.
Substituindo
Então a função também é solução da EDO.
Passo 2
Agora, precisamos determinar se existe uma solução que seja combinação linear das funções. Para isso, vamos ver se elas são linearmente dependentes calculando o wronskiano.
Derivando
Então, o wronskiano será:
Calculando o wronskiano
O wronskiano é diferente de 0. Logo, as funções são linearmente independentes.
Resposta
Exercícios de Livros Relacionados
Verifique que y = 1 x é uma solução para a equação diferencial não-linear y ' ' = 2 y 3 no intervalo ( 0 ,∞ ) .Mostre que um múltiplo y = c / x não é uma solução para a equação quando c ≠ 0 , ± 1 .
Nos problemas 33-40, verifique que as funções dadas formam um conjunto fundamental de soluções para a equação diferencial no intervalo indicado. Forme a solução geral. x 3 y ' ' ' + 6 x 2 y ' ' + 4 x
Verifique que y 1 = 1ey 2 = ln x é uma solução para a equação diferencial não-linear y ' ' + y ' 2 = 0 no intervalo ( 0 ,∞ ) . y 1 + y 2 é solução para a equação? c 1 y 1 + c 2 y 2 ,c 1ec 2 constant
Nos problemas 48 e 49, use os resultados do Problema 47.No capítulo 6, veremos que as soluções y 1ey 2 para x y ' ' + y ' + x y = 0 , 0x∞ , são séries infinitas. Suponha que consideremos as condições
Verifique que y 1 = x 3ey 2 = x 3 são linearmente independentes da equação diferencial x 2 y ' ' - 4 x y ' + 6 y = 0 em - ∞ ,∞ . Mostre que W y 1 ,y 2 = 0 para todo número real.O resultado da parte (b