Um corpo de massa é lançado da superfície da Terra. Seja a massa da Terra e o raio da Terra. Despreze a resistência do ar.
a) Qual a velocidade mínima requerida para mandar o projétil a uma altura de acima da superfície da Terra? Dê sua resposta em função de , e , onde é a constante gravitacional.
b) Considere agora a situação onde o projétil se mantém em órbita circular em torno da Terra a uma altura de acima da superfície. Calcule o módulo da velocidade do projétil. Dê sua resposta em função de , e .
c) Agora, calcule o módulo da velocidade de lançamento(a partir da superfície) necessária para que o projétil se mantenha em órbita circular a uma altura de acima da superfície terrestre. Dê sua resposta em função de , e .
Passo 1
Na letra (a), queremos achar a velocidade mínima para que o corpo alcance uma distância de .
Nesse processo de lançamento, a única força externa atuando no corpo é a força gravitacional. Como ela é uma força conservativa, podemos aplicar sem medo a conservação de energia:
Mas quem são as energias finais e iniciais?
No momento logo após o lançamento, o corpo tem uma energia cinética associada à sua velocidade.
Além disso, como o corpo está na superfície da Terra, ele tem uma energia potencial gravitacional associada à sua distância do centro da Terra.
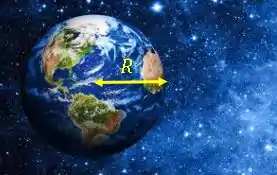
Mas, para o corpo ser lançado com a velocidade mínima suficiente para chegar à altura de , ele vai atingir esse ponto quando sua velocidade chegar a zero. Por isso, ele não terá mais nenhuma energia cinética, ela estará toda na forma de energia potencial gravitacional .
Lembrando que a distância agora será de , pois somamos o raio da Terra com a altura do corpo a partir da superfície.
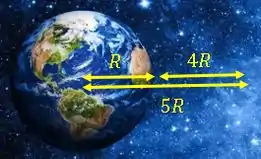
Então, conservando a energia, temos:
Assim, achamos que a velocidade mínima necessária é:
Passo 2
Vamos para a letra (b). Para achar a velocidade de um corpo em órbita circular, podemos igualar a força gravitacional à força centrípeta:
Novamente, como a altura a partir da superfície é , a distância do centro da Terra será :
Agora basta isolar a velocidade e correr pro abraço:
Passo 3
Na letra (c), queremos a velocidade de lançamento para que o corpo passe a orbitar na altura de .
Diferente da letra (a), o nosso corpo não vai chegar à altura de sem velocidade. Ele chegará à essa altura com uma velocidade suficiente para mantê-lo em órbita, que já calculamos na letra (b).
Portanto, faremos novamente uma conservação de energia, levando em consideração que temos energia cinética tanto no lançamento (inicial) quanto na órbita (final).
Sua velocidade de lançamento é (inicial), enquanto sua velocidade orbital é (final).
Substituindo o valor de :
Assim, achamos que a velocidade de lançamento necessária é:
Resposta
(a)
(b)
(c)