A figura abaixo ilustra um satélite de massa que está em movimento em uma órbita elíptica ao redor de um planeta de massa . O planeta encontra-se localizado em um dos focos da elipse (ponto ). As distâncias mínima e máxima entre o planeta e o satélite são, respectivamente, (distância entre o foco e o ponto , chamado periélio) e (distância entre o foco e o ponto , chamado afélio). Nestas condições:
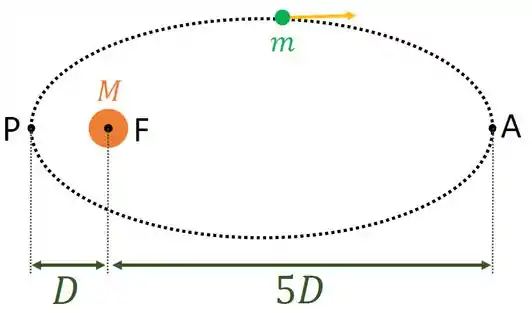
(a) Determine a razão entre a energia mecânica do sistema no ponto e a energia mecânica no ponto , isto é, .
(b) Calcule o módulo das velocidades do satélite nos pontos e .
Passo 1
Letra : Primeiramente, vamos lembrar algumas leis de conservação.
Para o nosso caso, vamos considerar que a massa do planeta seja muito maior que a do satélite (massa ), de forma que podemos considerar o planeta parado no ponto . Desta forma, considere a situação abaixo.
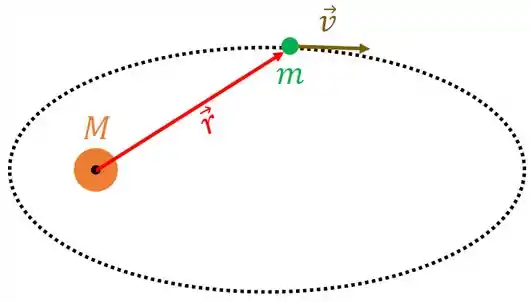
O vetor vai do planeta até o satélite. A interação relevante entre o satélite e o planeta é a gravitacional. Sabemos que a força gravitacional é uma força conservativa e radial. Assim, temos duas quantidades (temos mais, mas são duas que importam para gente) que se conservam: a energia mecânica total e o momento angular total.
A energia mecânica total do sistema é a energia do satélite interagindo com o planeta, que pode ser separada em duas partes: em sua energia cinética e sua energia potencial gravitacional, isto é,
com a constante de gravitação universal.
Já o momento angular total do sistema é o momento angular do satélite em torno do planeta. O mesmo é dado (em módulo) por
com o menor ângulo entre e .
Desta forma, no próximo passo, vamos resolver o item (a). Simbora!
Passo 2
Letra : Como foi comentado no passo 1, a força gravitacional é uma força conservativa. Isto faz com que a energia total do sistema seja conservada sempre. Assim, para qualquer ponto da trajetória do satélite,
Desta forma, considere os pontos e . Como a conservação é para todos os pontos, temos que
isto é, a energia mecânica total no ponto é igual a energia mecânica total no ponto . Deste modo, temos imediatamente que
Passo 3
Letra : Neste passo, aplicaremos as equações de conservação para determinar e .
Sabemos que o momento angular total do sistema é conservado (pois a força gravitacional é uma força radial). Deste modo, temos que, nos pontos e
Podemos visualizar o sistema quando passa por este pontos. Veja abaixo.
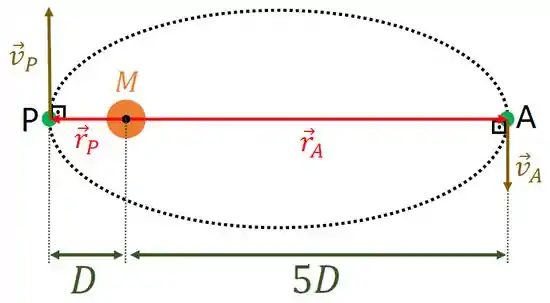
Da figura anterior, vemos imediatamente que
Desta forma, temos da equação de conservação de momento angular,
Agora, da equação de conservação de energia mecânica, temos que
Substituindo , temos que
Podemos agora determinar . Como , temos que