UTFPR - Pato Branco - Física 1 - Listas - Teste 9 - Listas Prof. Marcelo Sandrini - Lista 4 - Questão 12
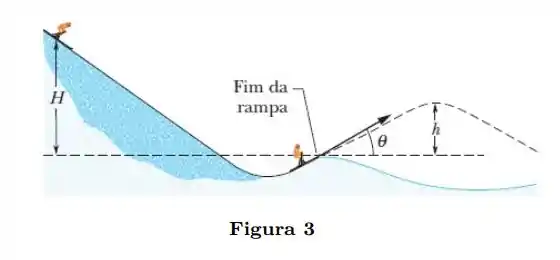
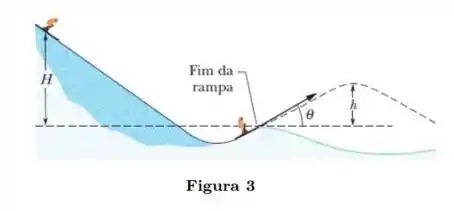
Um esquiador de parte do repouso a uma altura acima da extremidade de uma rampa para saltos de esqui (Fig. 3), e deixa a rampa fazendo um ângulo de com a horizontal. Despreza os efeitos da resistência do ar e suponha que a rampa não tem atrito. Qual é a altura máxima do salto em relação a extremidade da rampa? Se o esquiador aumentasse o próprio peso colocando uma mochila nas costas, seria maior, menor ou igual?
Passo 1
Oiie, tudo bem?
Temos nesta questão um esquiador de massa , que está no topo de um plano inclinado de altura . No final deste plano inclinado, temos uma rampa que faz com que após a descida, o esquiador seja lançado obliquamente em um ângulo de com a horizontal. Durante este movimento o esquiador irá alcançar uma altura máxima que devemos calcular na alternativa e então analisar a diferença que mudanças na massa do esquiador faria ao valor calculado! O sistema descrito é tal que
Vamos usar as leis de conservação da energia mecânica para obter a velocidade inicial com a qual o esquiador é lançado, e novamente, para determinar a altura máxima atingida, ou seja, vamos utilizar basicamente que
Para forças conservativas! O que é o caso da força gravitacional! Vamos lá!
Passo 2
Se o esquiador está inicialmente em repouso, temos que sua energia cinética inicial é zero e, estando em uma altura , temos que a sua energia potencial inicial é . Se considerarmos que a ponta da rampa é o ponto de energia potencial nula, ou seja, , temos que a energia cinética ganha será
que será igual a
E portanto, temos que
Resolvendo o produto obtemos que . E, se utilizarmos a definição de energia cinética como
Podemos isolar a velocidade para obter
Maravilha! Agora o que podemos fazer com essa velocidade? Ela será uma energia cinética inicial em uma segunda conservação de energia! Conseguiu visualizar? Vem comigo!
Passo 3
Agora, temos que inicialmente temos uma energia cinética de , como vimos no passo anterior, neste mesmo ponto a energia potencial é nula pela nossa escolha de referencial. A altura máxima que o corpo irá chegar está relacionada à uma altura máxima , obtida quando o corpo para de se mover para cima e começa a cair. Isso acontece quando a energia cinética total é igual a ?
NÃO! Note que horizontalmente o sistema não sofre a influência de nenhuma força, portanto, o corpo ainda terá velocidade em sua altura máxima! No entanto, a componente vertical da velocidade será nula! Desta forma, precisamos saber quanto da energia cinética inicial é devido a componente vertical da velocidade! Pois essa é a energia gasta ao levarmos a partícula até a altura . Mas como achamos essa componente vertical?
Temos o seguinte triângulo retângulo formado pelo vetor velocidade inicial e ângulo do lançamento oblíquo
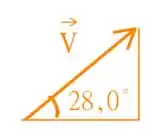
Note que como a hipotenusa é dada pelo módulo da velocidade inicial, que achamos no passo anterior como , e como temos que o cateto oposto deste triângulo é a componente vertical da velocidade, podemos obter a componente usando que
E, portanto, a nossa componente vertical será
Ou seja, a energia cinética que será transformada em potencial pelo trabalho da força gravitacional será
Colocando em uma calculadora, temos que
Vamos agora aplicar a conservação da energia! Belezinha? Bora lá!
Passo 4
Temos que inicialmente e . Na altura máxima temos que a energia cinética vertical toda se transforma em potencial, portanto, temos que
Utilizando que , temos que
ou seja
E a altura máxima será
Agora, será que mudar a massa do esquiador fará alguma diferença? Não, não fará! Note que a lei de conservação de energia em termos gerais é
Todos os termos contém a massa , e esse termo é irrelevante, portanto, adicionar mais massa ao esquiador não mudaria a altura máxima no caso sem atrito ou resistência do ar. A questão foi isso! te vejo na próxima! Tchau Tchau!