Uma pedra de massa caindo em queda livre é capturada por uma pessoa de inércia . Ao atingir a mão da pessoa a pedra tem velocidade , e durante a captura o braço da pessoa se desloca verticalmente para baixo por uma distância . Considerando um sistema formado pela pedra+planeta, calcule o trabalho realizado por cada força externa que age no sistema entre o instante que a pessoa inicia o movimento de captura da pedra até o instante que a pedra para na mão da pessoa. Escreva a Lei de conservação de Energia do sistema pedra+planeta.
Passo 1
Bem, o sistema é formado apenas pela pedra e pela Terra...
A pessoa, certamente é um agente externo a esse sistema...
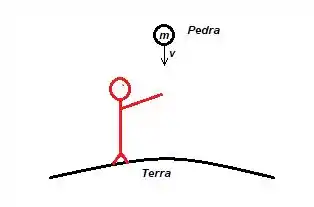
E quando a pedra chegar na mão da pessoa, ela vai fazer uma força (força pedra-pessoa) direcionada para cima deslocando a mão da pessoa de ...
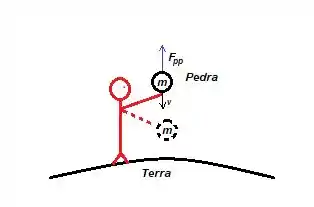
Então repare que a única força que se intromete no sistema é a força que a pessoa faz na pedra para pará-la! Logo, se queremos o trabalho de todas as forças externas. Temos que ficar atento, pois a única que realmente vai ter um trabalho diferente de vai ser a força . E pela nossa teoria de trabalho (força vezes deslocamento)
O menos é só porque a força está apontando para cima que é contrário ao deslocamento.
“AH! Mas essa é a única força externa?”
Passo 2
A única que não é nula sim. Afinal de contas existem outras forças externas, mas elas não interferem no deslocamento , então o trabalho delas é nulo. As duas outras forças a qual me refiro é a peso da pessoa () e a força normal ...
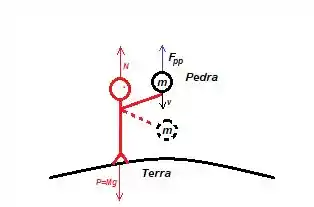
Mas como eu disse, o trabalho dessas forças é nulo já que eles não interferem no deslocamento da pedra:
Logo, o trabalho total das forças externas será...
Passo 3
Beleza! Agora temos que escrever a Lei de conservação de Energia do sistema pedra+planeta.
POW! Sabemos que a energia do sistema pode ser dada pela Teoria como a soma da energia cinética com a energia interna ...
Se fosse um sistema sem forças externas, a variação da energia do sistema seria ...
Mas como tem interferência de forças externas, podemos dizer que a variação da energia do sistema pela Lei da conservação então vai ser igual ao trabalho externo...