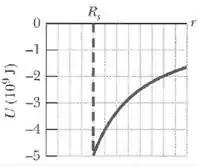
A figura mostra a energia potencial de um projétil em função da distância da superfície de um planeta de raio . Se o projétil é lançado verticalmente para cima com uma energia mecânica de , quais são sua energia cinética a uma distância e seu ponto de retorno em termos de ?
Passo 1
Bora lá, galera do nosso Brasil!
Isso é um problema de conservação de energia. Como eu sei disso? Só ver,de cara, que ele fala em energia potencial, energia cinética e energia mecânica. Daí agora é só procurar relacionar essas grandezas por meio da conservação da energia.
Deu pra entender? Então vem comigo! :}
Passo 2
(a) Ele fala que a energia mecânica é de . Assim, pelo conceito de energia mecânica, teremos:
Ah! Olhando no gráfico, na posição de , teremos isso aqui:
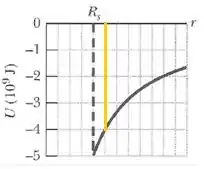
Plim! A energia potencial em é .
Usando nossa equaçãozinha lá, teremos:
(b) Agora vamos calcular o ponto de retorno em termos de .
O ponto de retorno é o ponto no qual a energia cinética do projetil será igual a zero.
Logo:
Pegando o ponto do gráfico (), temos:
Substituindo na equação de cima:
É isso aí! :P