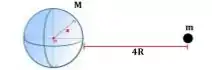
Uma partícula pontual de massa está a uma distância da superfície de uma esfera de massa e raio , conforme ilustrado na figura abaixo. Se mantivermos a esfera fixa e soltarmos a partícula do repouso, deixando que a força gravitacional desloque a partícula em direção à esfera, com que velocidade a partícula atingirá a superfície da esfera? Nas respostas abaixo, significa a constante universal da gravitação.
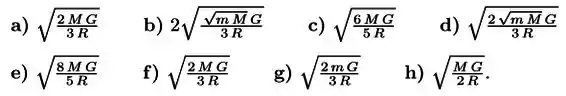
Passo 1
Essa questão temos que resolver por conservação da energia mecânica.
No inicio ela está parada. Assim só há energia potencial, preste atenção que a distância entre o centro da esfera e a partícula é de .
Agora, pela conservação de energia temos que
A energia potencial final é a energia potencial da partícula na superfície da esfera.
Assim, a nossa equação fica
Agora que sabemos a energia cinética da partícula ao atingir a superfície da esfera, conseguiremos descobrir a velocidade dela
Assim, a velocidade é escrita como:
Substituindo o valor da da energia cinética, temos:
Resposta