4. Seja uma função que satisfaz as seguintes condições:
- é contínua
- O gráfico da derivada de é dado pela figura abaixo.
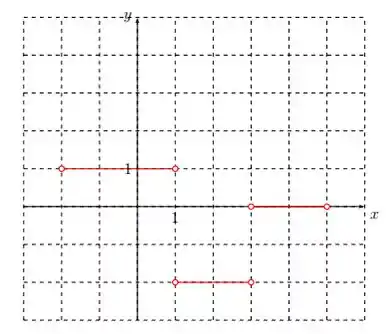
Faça o gráfico de .
Passo 1
Olá, galerinha! Tudo bom? Aqui temos que desenhar um gráfico seguindo algumas condições.
A primeira delas é que a função seja contínua no intervalo dado. De forma prática, o que precisamos fazer é desenhar o seu gráfico sem tirar o lápis do papel. Fazendo isso, respeitamos a condição de continuidade.
A segunda condição é que , ou seja, precisamo que a função passe pelo ponto .
Por fim, temos o gráfico da derivada de Repara que ele são constantes. Então para desenhar o gráfico, temos que lembrar que a derivada é a variação de em relação a .
Como todas as partes da função são lineares, podemos calcular essa variação pelo delta, ou seja,
Agora temos que plotar esses deltas de acordo com cada intervalo.
Bora lá!
Passo 2
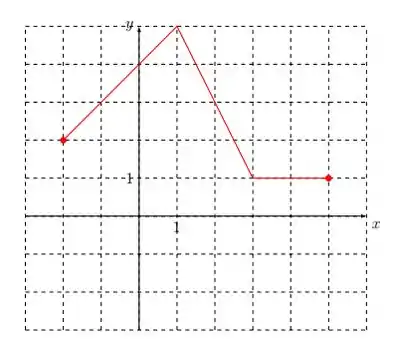
No primeiro intervalo, temos que , temos que a . Além disso, sabemos que . Então precisamos traçar uma reta com o coeficiente angular igual a , que passe por esse ponto.
Sendo assim, temos que ligar os pontos até , para respeitarmos essa condição.
Para o segundo intervalo de , temos que . Ou seja, precisamos traçar uma reta com o coeficiente angular igual a . E para respeitar a condição de continuidade, temos que essa reta tenha que partir de . Logo, ela ira terminar em .
Para ultimo intervalo , a derivada é zero. Se a derivada neste invervalo é nula, significa que temos uma função constante, neste intervalo. Para manter a nossa continuidade, temos que a partir daí a função será igual a .
Plotando tudo, ficamos com
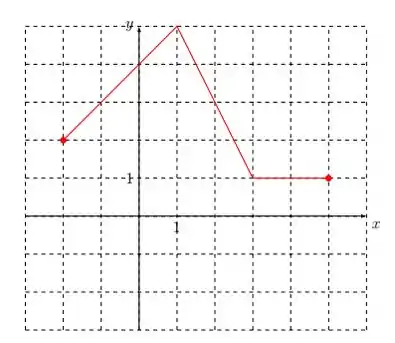
Resposta