Funções de Várias Variáveis, Limites e Continuidade, Derivadas Parciais e o Vetor Gradiente
Seja
a) Esboce, no sistema de coordenadas cartesiano, as curvas e nível e de .
b) A função é contínua em ? Justifique.
c) Determine, caso exista, .
Passo 1
a) Curvas de nível? Basta pegar a função e igualar ao nível e descrever a curva!
Vamos fazer isso para o primeiro nível? Fica:
Desenvolvendo,
Passando o para o lado esquerdo, temos:
Completando o quadrado para o , somando e subtraindo , fica:
Colocando o quadrado correspondente para o termo entre os parêntesis e passando o para o lado direito, fica:
Multiplicando tudo por , teremos:
E aí está a equação da nossa curva!
Passo 2
Vamos esboçá-la? Como temos e elevados ao quadrado, mas subtraídos um do outro, trata-se de uma hipérbole. Como o sinal positivo está no , então ela tem as bocas apontadas para ele. Além disso, e na sua equação, logo, está centrada em .
Pra ver os pontos que a curva corta o eixo , façamos :
Logo, ela corta o eixo em ou !
Seu esboço fica:
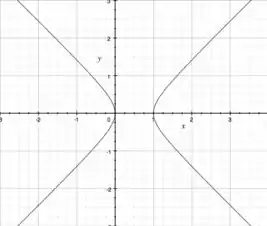
Passo 3
Show, agora vamos fazer a mesma coisa para a curva de nível ! Pare de ver a resolução e tente fazer por conta própria, é exatamente a mesma coisa :D
Vou escrever qualquer coisa aqui só pra você não ver o passo
Vou escrever qualquer coisa aqui só pra você não ver o passo
Vou escrever qualquer coisa aqui só pra você não ver o passo
Vou escrever qualquer coisa aqui só pra você não ver o passo
Vou escrever qualquer coisa aqui só pra você não ver o passo
Tá acho que já deve ter dado....
Passo 4
Beleza! Vamos lá, temos que começar igualando a função ao nível em questão:
Passando o para o lado direito, fica:
Passando, agora, o para o lado esquerdo,
Completando o quadrado...
Passando o pra direita e escrevendo o quadrado correspondente,
Show! Fechou a equação!
Passo 5
Novamente, temos uma hipérbole, pois as duas variáveis estão ao quadrado e com sinais trocados! Como o positivo está no , ela abres as bocas para ele! Observando que , então ela é centrada nesse ponto.
Pra ver os pontos que a curva corta o eixo , façamos :
Logo, ela corta o eixo em ou !
Por fim, seu esboço:
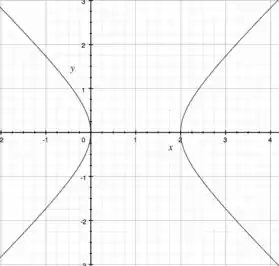
Passo 6
b) Ok, chegou a hora de ver se a função é contínua em ... Para isso, devemos verificar se o limite quando tendemos à origem é o mesmo que o valor que ela assume nesse ponto, ou seja, se esse limite vale !
Mas... calma aí... Você percebeu algo de estranho nos gráficos que desenhamos para as curvas de nível?
Você viu que, para os dois níveis que esboçamos, aparece em ambos? Sim, isso significa que, para um mesmo e um mesmo , no caso, , temos dois valores para !
Em outras palavras, colocando na função, temos ou ! Mas isso é impossível de acontecer numa função, pois, dada uma entrada, só podemos ter uma saída! Essa é a prova mais concreta que poderíamos esperar de que o limite não existe quando tendemos à origem, logo, ela não é contínua!
Passo 7
c) Partiu calcular essas derivadas! Vamos ter que usar a definição delas pelo limite...
Para a derivada em relação a , basta resolver:
Colocando o valor de e , temos:
E, assim, a derivada em relação a vale !
Passo 8
Para a derivada em relação a , basta resolver:
Colocando os valores de e ,
Repara que tanto quando vamos ter então nos dois casos temos zero, por isso nosso limite fica no numerador.
E, então a derivada em relação a é !
Assim, o vetor gradiente fica:
E é isso aí :D Terminamos a primeira questão! Partiu questão !
Resposta
a) Curva de nível :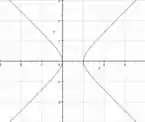 
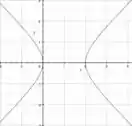
b) A função não é contínua
c)