Seja
1. Faça um esboço do conjunto
2. Determine se a função é contínua na origem.
3. Calcule, se existirem, as derivadas parciais e .
Passo 1
1. Vamos traduzir aquelas notações ali. Ele quer que a gente esboce . Quem é Essa função:
A gente acha , se igualar ela a :
Como está no , a gente sabe que é uma curva. Aí vamos completar quadrados para entender que curva é essa.
Cara, isso é uma circunferência. Comparando com a equação geral da circunferência de raio e centro :
Ela tem centro e raio . Aí desenhando uma circunferência com essas características:
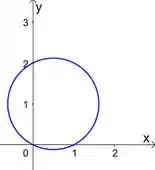
Mas será que é só isso mesmo?
Passo 2
Não é não! Ao desenhar , a gente está fazendo uma curva de nível de em . E ao fazer curvas de nível, a gente precisa representar o domínio da nossa função.
Como assim? Aquela expressão para que a gente usou
Só vale para . Então a curva que a gente achou a partir dela não está definida na origem. Aí na verdade, nosso esboço é aberto nesse ponto:
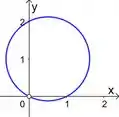
Como em , , a origem realmente não pertence a nossa curva, que é o conjunto dos pontos onde . Então nosso esboço fica assim mesmo.
Passo 3
2. Olha para dizer se uma função é contíninua nesse ponto a gente precisa que o limite:
Exista e seja igual a . Bora verificar isso.
Podemos usar o caminho nesse limite, para provar que ele não existe. Por que? Cara, o grau do numerador é menor do que o do denominador, então a gente vai suspeitar que ele não existe.
Fica assim:
Ih como o denominador zerou, o limite foi para infinito. Isso significa que esse limite não existe. E assim, nossa função não é contínua nesse ponto.
Passo 4
3. Como a nossa função muda de definição no ponto , a gente vai ter que usar a definição de derivadas parciais. Para a derivada em relação a :
E a definição da função diz que :
Passo 5
A derivada em relação a fica bem parecida:
Como os dois limites explodiram para infinito, a gente vai dizer que as nossas derivadas parciais não existem na origem.
Resposta
a) 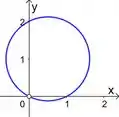
b) A função não é contínua na origem.
c) As derivadas parciais não existem na origem.