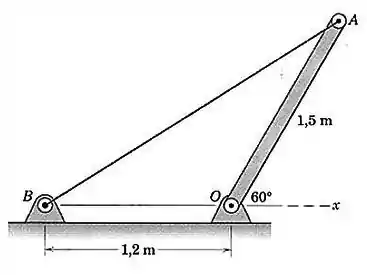
A barra uniforme com é mantida na posição mostrada por um pino liso em e pelo cabo . Determine a força trativa no cabo e o módulo e a direção da reação externa no pino em .
Passo 1
O diagrama de corpo livre dessa estrutura é:
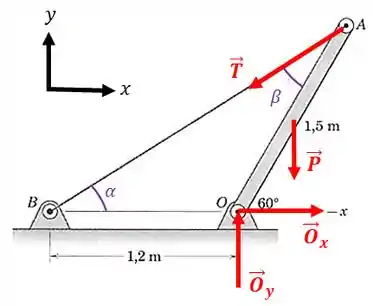
Passo 2
Para achar as reações, temos que começar fazendo o somatório de momentos com relação a um ponto. Mas qual ponto vamos escolher?
Aquele que tenha alguma das nossas incógnitas. Dessa forma, eliminamos alguma das incógnitas, já que a força que está bem em cima do ponto que escolhermos não possui braço de alavanca.
Vamos escolher o ponto .
Mas antes temos que calcular as distâncias das forças até o ponto .
Passo 3
Vamos começar achando os ângulos e . Para isso, vamos formar o seguinte triângulo retângulo:
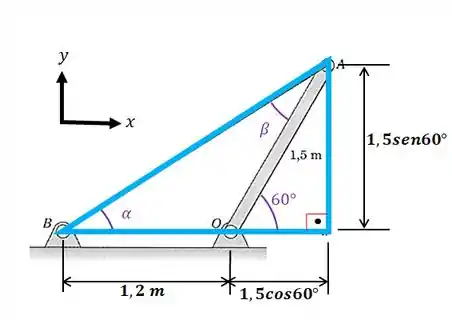
Temos que o ângulo é:
Passo 4
Sabendo o ângulo podemos decompor a força trativa :
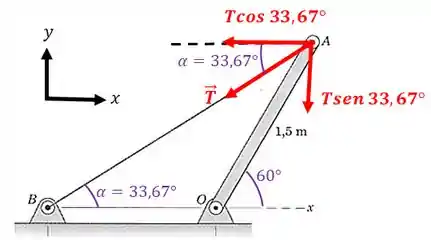
E as distâncias de cada componente com relação ao ponto são:
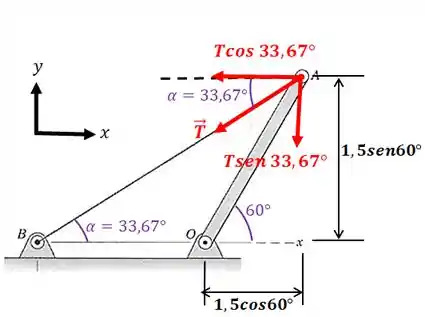
Passo 5
Agora vamos achar a força peso:
E a distância dela até o ponto ? Vamos fazer o seguinte triângulo retângulo:
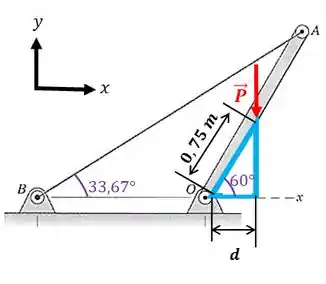
Repare que a força está posicionada na metade da barra de , ou seja, está a . Então, a distância é:
Passo 6
Agora sim podemos calcular o somatório de momento com relação ao ponto . Para isso vamos considerar o momento positivo no sentido anti-horário:
Passo 7
Agora vamos fazer o somatório de forças horizontais:
Repare que o sinal deu positivo. Isso significa que arbitramos o sentido da reação certinho.
Passo 8
Agora vamos fazer o equilíbrio das forças verticais:
Passo 9
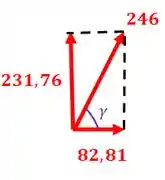
Agora temos que achar a resultante no apoio :
Agora temos que saber o ângulo que a resultante faz com relação ao eixo :