Responde Aí
Acesse com GoogleAcesse com AppleAcesse com Facebook

Exercícios Resolvidos de Equilíbrio em duas Dimensões

Ver Teoria
Exercício 1812345678910111213141516171920212223

Enunciado

UFRJ, Mecânica 1, 2020.2, PF, Q1

Seja a torre abaixo, com altura 70 m, sustentada por três cabos:

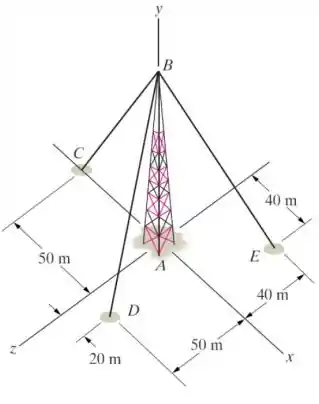
Pede-se:

  1. Desenhe o Diagrama de Corpo Livre da Estrutura, considerando a base da torre como um engaste. Observe que a torre pode ser tratada como uma coluna única, ou seja, a base da torre pode ser representada por um único ponto.
  2. Considerando que a tração no cabo BC é 5 kN, calcule as trações nos outros dois cabos para que o momento na base da torre seja nulo.

Passo 1

Primeiramente, observe que as forças atuando sobre a torre são as trações dos cabos (na direção dos cabos) e a reação tridimensional em sua base, que as compensa. Feito o Diagrama, para calcular o momento das forças em relação a A , deveremos considerar:

M → A = ∑ F i → × r i →

Onde r i → é o vetor que parte de A e vai ao ponto de aplicação da força F i → . Dessa forma, as forças de reação na base não terão momento e para as forças de tração r → = 0 ,   70 ,   0 .

Segue à obtenção do momento, fazermos M → A = 0 para determinar as forças de tração.

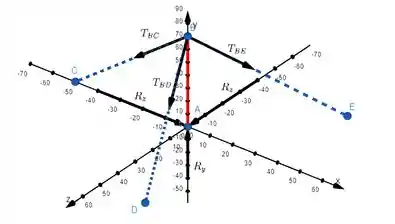
Figura 1: Diagrama de Corpo Livre da Torre AB

Passo 2

Em seguida, para calcular

M → A = ∑ F i → × 0,70,0

= ∑ F i → × ( 0,70,0 )

Precisamos determinar as forças enquanto vetores, o que faremos utilizando os cabos como suporte para determinar as direções:

r B C → = B C →   B C → = C - B   B C → = - 50,0 , 0 - 0,70,0 B C → =    

= - 50 , - 70,0 50 2 + 70 2 = 1 84 - 5 , - 7,0 =

= 1 2 21 - 5 , - 7,0  

E ainda,

r B D → = B D →   B D → = D - B   B D → = 20,0 , 50 - 0,70,0 B D → =    

= 20 , - 70,50 20 2 + 70 2 + 50 2 = 1 88 ( 2 , - 7,5 )  

= 1 2 22 ( 2 , - 7,5 )

Bem como,

r B E → = B E →   B E → = E - B   B E → = 40,0 , - 40 - 0,70,0 B E → =    

= 40 , - 70 , - 40 40 2 + 70 2 + 40 2 = 1 81 ( 4 , - 7 , - 4 )  

= 1 9 ( 4 , - 7,4 )

Logo,

T B C → = T B C r B C → ,                 T B D → = T B D r B D → ,                 T B E → = T B E r B E →

Passo 3

Agora, o momento pode ser calculado:

M → A = ∑ F i → × ( 0,70,0 )

= T B C r B C → + T B D r B D → + T B E r B E → × ( 0,70,0 )

= - 5 2 21 T B C + 2 2 22 T B D + 4 9 T B E , - 7 T B C 2 21 - 7 2 22 T B D - 7 9 T B E , 5 2 22 T B D - 4 9 T B E × ( 0,70,0 )

= i j k 0 70 0 - 5 2 21 T B C + 2 2 22 T B D + 4 9 T B E - 7 T B C 2 21 - 7 2 22 T B D - 7 9 T B E 5 2 22 T B D - 4 9 T B E =

= 70 5 2 22 T B D - 4 9 T B E ,   0 , 5 2 21 T B C - 2 2 22 T B D - 4 9 T B E  

Passo 4

E igualado a 0 :

M → A = ( 0,0 , 0 ) ⇒

⇒ 5 2 22 T B D - 4 9 T B E = 0 5 2 21 T B C - 2 2 22 T B D - 4 9 T B E = 0 T B C = 5   k N ⇒ 4 9 T B E = 5 2 22 T B D 2 2 22 T B D + 4 9 T B E = 2 5 2 21  

⇒ 4 9 T B E = 5 2 22 T B D 2 2 22 T B D + 5 2 22 T B D = 25 2 21   ⇒ T B E = 45 8 22 T B D 7 2 22 T B D = 25 2 21  

⇒ T B E = 45 8 22 T B D T B D = 25 22 7 21   ⇒ T B E = 45 8 22 ⋅ 25 22 7 21 T B D = 25 22 7 21  

⇒ T B E = 1125 56 21 = 4,3838   k N T B D = 25 22 7 21 = 3,6555   k N  

Resposta

T B E = 4,3838   k N T B D = 3,6555   k N  

Exercícios de Livros Relacionados

Exercício de Livro
O comprimento não deformado da mola A B é 3m . Se o bloco é mantido na posição de equilíbrio mostrada, determine a massa do bloco em D .
O suporte deslizante é usado para apoiar partes de chapas longas enquanto elas são cortadas por uma serra de bancada. Se a chapa exerce uma força direcionada para baixo de 25N no rolete C , determine
O guincho é usado para suspender o motor de 200k g . Determine a força que atua no cilindro hidráulico A B , as componentes horiozntal e vertical da força no pino C e as reações no apoio fixo D .
Todos as soluções dos problemas precisam incluir um diagrama de corpo livre.F5.3. A treliça é suportada por um pino em A e um rolete em B. Determine as reações dos apoios.