O centro de massa do carro de motor traseiro e com está localizado como mostrado na figura. Determine a força normal sob cada pneu quando o carro está em equilíbrio. Descreva qualquer hipótese feita.
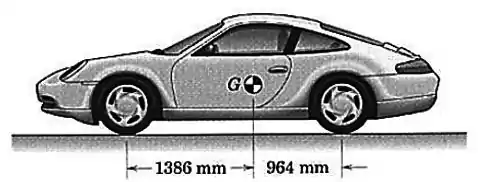
Passo 1
O sistema acima pode ser desenhado assim:
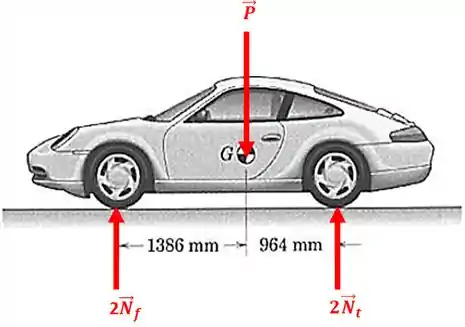
Onde, é a força peso, é a força normal na roda da frente e é a força normal na roda de trás.
Mas por que colocamos e Porque o carro tem quatro rodas e cada roda tem a sua força normal. Então, admitimos que o carro é simétrico e que a outra metade dele vai ter a mesma configuração de forças.
Passo 2
O carro possui , então o módulo da força peso será:
Agora vamos fazer o equilíbrio dessas forças:
Precisamos de outra equação para resolver o problema. Vamos fazer o somatório de momentos com relação ao ponto indicado na figura abaixo:
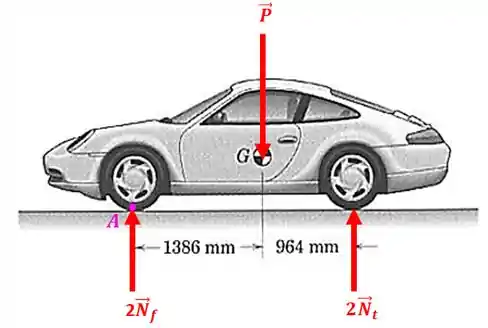
O equilíbrio de momentos em relação ao ponto nos dá:
Voltando para a equação do equilíbrio das forças, podemos substituir o valor de que achamos: