1) A peça BCD do guindaste é ligada à peça AC por meio de rótula no ponto C. O conjunto está articulado nos pontos A e B. O peso das peças é desprezível frente ao peso da massa , igual a . O raio das polias e do tambor no ponto E está indicado no desenho. As cotas indicam distâncias em metros entre centros de polias, apoios ou ligações.
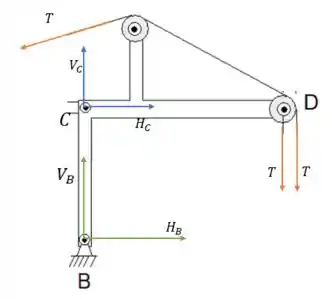
a) Desenhe o(s) diagrama(s) de corpo livre necessários para a determinação das reações de apoio.
b) Determinar a magnitude da força de reação no ponto B em unidade kN, com duas casas decimais.
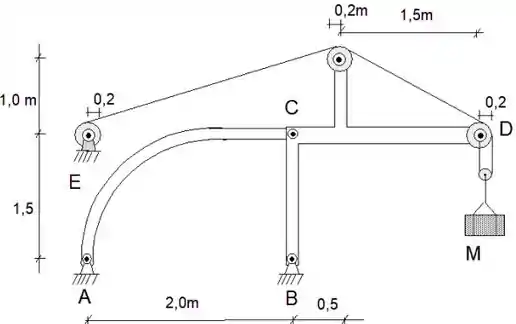
Passo 1
Faaaala galera do Responde Aí! Tudo certinho com vocês?
Temos uma questãozinha bem interessante da parte de estática da mecânica.
a) Pra começar, precisamos desenhar os diagramas de corpo livre que serão necessários para a determinação das reações de apoio.
O primeiro passo é determinar quem serão os corpos livres que desenharemos os diagramas visando encontrar as reações de apoio. A ideia aqui é separar os corpos que podem ser separados, pois a estrutura formada nessa questão é a junção de 4 peças distintas: AC, BCD, carga M e corda e polia em E.
Nesses casos separar é útil porque essas peças também devem estar em equilíbrio separadamente, logo, fazendo isso conseguimos escrever equações de equilíbrio com menos variáveis, com resoluções bem mais simples.

Beleza! Agora que já sabemos do que desenhar os DCL’s, só devemos nos atentar que pares de ação e reação possuem sentidos opostos, além de que as barras articuladas possuem reações nos dois eixos.
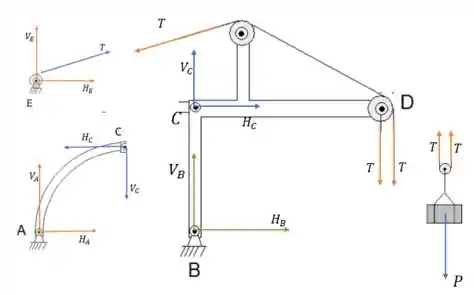
Prontinho, desenhamos os quatro diagramas que vamos precisar 😊
Passo 2
b) Nesse item devemos determinar a magnitude da força de reação em B, ou seja, o valor da intensidade da resultante das reações em B.
Para isso, vamos usar os nossos diagramas para extrair as equações necessárias.
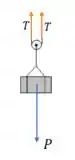
Para que haja o equilíbrio de forças na vertical, devemos ter que:
Beleza, lembrando que , mas vamos deixar para substituir os números apenas no final.
Agora vamos analisar o DCL da peça AC:
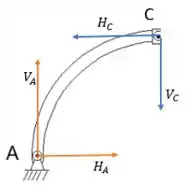
Como o momento em A deve ser nulo (pois estamos em equilíbrio estático), e os braços de e em relação a A valem ambos m e m, respectivamente, vem que:
Esse resultado é muito bom! Conseguimos eliminar mais uma variável do nosso problema.
Vamos analisar agora o último diagrama antes de determinar a reação.
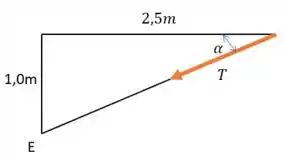
Como as únicas variáveis (além de ) que não conhecemos o seu valor estão em B são e , bora calcular o momento justamente em relação a esse ponto. Mas antes disso, vamos decompor a tração agindo em E, para que fique mais fácil determinar o braço da força.
Sendo o ângulo entre a direção da tração em E e a horizontal, temos:
Beleza! Voltando para o DCL, temos que o momento em relação a B também deve ser nulo. Logo:
Usando que, pelo triângulo mostrado acima:
Logo:
Usando , vem:
Como encontramos , temos que:
Top pessoal! Agora que encontramos as reações em C, podemos usar o mesmo DCL de CBD para calcular as resultantes em na vertical e horizontal, pois como sabemos deve valer que:
Massa demais! Estamos quase terminando, pois já conseguimos determinar as reações em B. Para calcular a resultante, basta usarmos o nosso teorema de Pitágoras. Daí, vem que:
Como a resposta é pedida em kN com duas casas decimais, temos que:
Aí sim gente! Matamos mais uma questão. Espero que todos tenham entendido direitinho. Já vamo aquecer pra próxima, até lá!!
Resposta
a) Resolução no texto.
b)