02) A figura mostra a seção transversal de um reservatório, de largura (ortogonal ao plano da figura), projetado para armazenar um fluido ideal de densidade (kg/m³). O fluido é mantido no reservatório por meio da comporta AOB, de massa desprezível, articulada em e apoiada no solo em A, sem atrito. A altura máxima de fluido que pode ser armazenado no reservatório é controlada por um contrapeso, de massa (kg), situado na extremidade B da comporta. A aceleração da gravidade é (m/s²). Nestas condições, pede-se:
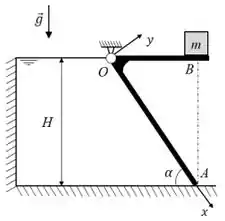
a) Construir o diagrama de forças hidrostáticas atuantes sobre a superfície AO;
b) Determinar a resultante do sistema de forças hidrostáticas considerado no item a).
c) Determinar a abscissa do centro de pressões do sistema de forças hidrostáticas considerado no item a);
d) Desenhar o diagrama de corpo livre da comporta AOB;
e) Determinar o esforço atuante no ponto de apoio A;
f) determinar o valor mínimo da massa do contrapeso necessária para manter o sistema sempre em equilíbrio estático.
Passo 1
Ooi gente, tudo bom com vocês?
a) O primeiro item desse exercício pede pra gente construir o diagrama de forças hidrostáticas na superfície AO.
Sabemos que um fluido exerce uma pressão na superfície AO a qual é sempre perpendicular à superfície e pode ser escrita como:
Assim, vemos que a pressão cresce linearmente com a altura (profundidade) do fluido.
Mas, sabendo que , então tomando um pequeno elemento de área , onde , temos:
Logo, para cada nível de altura temos uma força que é proporcional a essa altura. É como se tivéssemos um carregamento triangular sobre a barra . Já podemos então desenhar o diagrama forças hidrostáticas:
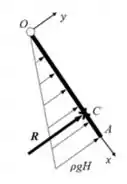
De fato, em A, onde , temos: .
Prontinho 😊
Passo 2
b) Aqui precisamos calcular a resultante de forças desse carregamento. Sendo bem rigoroso com a teoria, temos que:
Outra forma de fazer é calcular o volume do prisma do carregamento triangular.
Passo 3
c) Basicamente, queremos saber a coordenada onde a resultante está sendo aplicada.
A resultante deverá ser aplicada na projeção do baricentro da superfície da seção transversal do prisma de pressões do item A. Assim, como o baricentro fica a do vértice oposto, temos:
Beleza!! Bora pra próxima!
Passo 4
d) Nesse item precisamos determinar o diagrama de corpo livre da comporta AOB, então vamos nos atentar a alguns detalhes. A resultante hidrostática já está atuando perpendicularmente à superf[icie AO.
Além disso, no ponto D temos reação tanto na vertical como na horizontal, já em A a barra está apenas apoiada, logo temos apenas reação na vertical. Por fim, em B temos a força peso de B atuando no bloquinho. Juntando tudo, podemos desenhar:
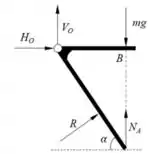
Passo 5
e) Aqui precisamos determinar o esforço atuante no ponto A. A dica é usarmos o fato de a estrutura estar em equilíbrio estático. Devido a isso, qualquer ponto escolhido também deverá estar em equilíbrio.
Por isso, vamos colocar o nosso polo em O:
Prontinho 😊
Passo 6
f) Devemos determinar a massa do contrapeso de modo que o sistema esteja sempre em equilíbrio estático. Para que isso ocorra, precisamos manter a haste fixa, o que ocorre apenas enquanto . Daí:
Ufaa, terminamos mais uma! Já vamos no embalo fazer a próxima questão. Valeu pessoal, tamo junto! 😉
Resposta
a) Resolução no texto
b)
c)
d) Resolução no texto
e)
f)