03) Considere o sistema em equilíbrio indicado na figura, composto pela estrutura de 5 barras ABCD, pelos blocos H e I, pelas polias ideais E, F e G e por fios também ideais. Os pesos dos blocos H e I são 10P e 8P, respectivamente. Os demais componentes do sistema têm peso desprezível. Há ainda uma força vertical de magnitude 4P aplicada na articulação, conforme mostrado na figura. O bloco 1 encontra-se apoiado em uma superfície plana inclinada de 45° com relação à horizontal. Pede-se:
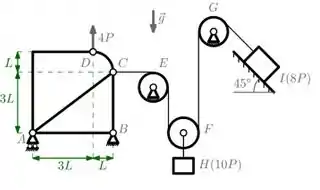
a) Os diagramas de corpo livre da estrutura composta por 5 barras ABCD, das polias E, F e G e dos blocos H e I.
b) As reações no apoio em A e na articulação em B.
c) As forças internas às barras AB, BC e AC indicando se são de tração ou compressão.
d) O menor valor do coeficiente de atrito estático entre o bloco 1 e o plano inclinado a fim de assegurar o equilíbrio do sistema.
Passo 1
Eaí pessoal, tudo bem com vocês?
a) Pra começar essa questão, precisamos desenhar os diagramas de corpo livre (DCL) da nossa estrutura.
Iniciando pelas 5 barras ABCD, temos em A um apoio do 1° gênero (reação apenas vertical) e em B um apoio do 2° gênero (reação vertical e horizontal). Além disso, em C temos uma tração T puxando a estrutura, e em D temos uma carga externa de valor 4P.
Beleza, acompanharam? Já poderíamos desenhar o DCL dessa parte.
Para cada polia temos a tração T puxando-as e para o bloco descendo o plano inclinado temos além da tração, o seu peso, normal e atrito.
Massa! Desenhando os DCL teremos:
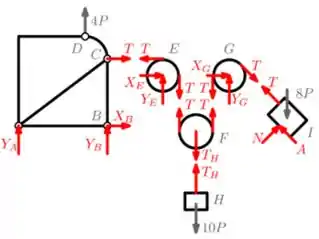
Prontinho 😊
Passo 2
b) Aqui precisamos descobrir as reações de apoio da estrutura de 5 barras ABCD.
Escrevendo as equações de equilíbrio na vertical e horizontal, temos que:
Fazendo o momento em relação ao ponto A, temos:
Beleza! Após encontrarmos essas equações, ficou evidente que precisamos determinar a tração no fio. Então, olhando o bloco H, temos:
Já pela polia F, temos:
Top! Substituindo esse valor nas equações encontradas anteriormente, teremos:
Muito bom! Conseguimos determinar as reações nos apoios. O sinal negativo em significa que o sentido proposto inicialmente está invertido.
Passo 3
c) Devemos encontrar o valor das forças internas nas barras AB, BC e AC. Como temos uma estrutura de treliça para as 5 barras ABCD, aplicando o método dos nós e supondo todas as barras inicialmente tracionadas, temos:
Nó B:
(compressão)
(compressão)
Nó C:
Dessas duas equações, sai que:
(Tração)
Eba! Foi mais uma letra, falta só a última agora.
Passo 4
d) Nos é pedido para calcular o menor valor do coeficiente de atrito estático de modo que o equilíbrio do bloquinho no plano inclinado esteja assegurado.
Daí, pelo DCL do bloquinho, podemos escrever que:
Da primeira equação, vem que:
Da segunda equação:
Na condição de atrito estático, devemos ter:
Na condição limite, temos o menor valor possível:
Aeeee, finalizamos mais uma questão! Espero que todos vocês tenham entendido bem direitinho.Até a próxima! 😊
Resposta
a) Resolução no texto.
b)
c)
(compressão)
(compressão)
(Tração)
d)