Responde Aí
Acesse com GoogleAcesse com AppleAcesse com Facebook

Exercícios Resolvidos de Equilíbrio em duas Dimensões

Ver Teoria
Exercício 2212345678910111213141516171819202123

Enunciado

USP, Mecânica, P1-2019.1, Questão 01

01) O cubo homogêneo ABCDA’B’C’D’, de lado 2 a e peso P , está sujeito ao sistema de forças indicado na figura abaixo. Utilizando a base de versores i → ,   j → ,   k → referentes aos eixos x ,   y ,   z , respectivamente, pede-se:

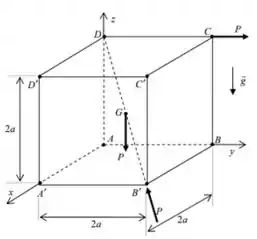
a) determinar a resultante do sistema de forças e o momento resultante em D;

b) determinar o momento resultante do sistema de forças no eixo AD;

c) determinar o momento resultante em A;

d) verificar se o sistema é redutível a uma única força.

Passo 1

Faaaala galera, tudo certinho?

a) Bom, pra começar precisamos transportar todas as forças para o ponto D. Assim, devemos descobrir a resultante de forças nesse ponto, bem como o momento resultante nesse polo.

Iniciando o cálculo pela resultante de forças, podemos escrever que:

R → = - P k → + P j → + P D - B ' D - B '

Beleza, mas quem é D - B ' ?

D = 2 a k →

B ' = 2 a i → + 2 a j →

Logo:

D - B ' =   - 2 a i → - 2 a j → + 2 a k →

Assim, vale:

D - B ' = - 2 a 2 + - 2 a 2 + 2 a 2 = 2 3 a

Substituindo na nossa resultante de forças, vem:

R D → = - P k → + P j → + P ⋅ - 2 a i → - 2 a j → + 2 a k → 2 3 a =   - 3 3 P i → + 3 - 3 3 P j → + 3 - 3 3 P k →    

Boa, a primeira parte já foi! Agora devemos calcular o momento resultante em D.

O bom é que apenas a força peso faz momento nesse ponto, pois a linha de ação das outras forças passa por D. Daí:

M → D = G - D × - P k →

Pela simetria do cubo, podemos afirmar logo de cara que:

G = a i → + a j → + a k →

⇒ G - D = a i → + a j → - a k →

Massa! Daí:

M → D = a i → + a j → - a k → × - P k → =   - a P i → + a P j →

Excelente! Conseguimos determinar a resultante de forças e de momento em D. Bora pro próximo item!

Passo 2

b) Aqui devemos terminar o momento resultante de forças no eixo AD. O eixo AD coincide com a direção k → . Logo, pra determinar M → A D basta a gente pegar essa componente pelo produto escalar:

M → A D = M → D ⋅ k → = - a P i → + a P j → ⋅ k → = 0

Portanto, não tem componente do momento resultante nesse eixo.

Passo 3

c) Agora devemos calcular o momento resultante em A.

A boa notícia é que não precisamos partir do início e calcular o momento que cada uma das forças faz em A, pois podemos usar direto a nossa resultante em D junto com o momento nesse ponto, de modo que vale:

M → A   = M → D + D - A × R → A

⇒ M → A = - a P i → + a P j → + 2 a k → × - 3 3 P i → + 3 - 3 3 P j → + 3 - 3 3 P k →    

Pois é, muitas contas, mas não tem o que fazer. Então, resumindo vamos chegar que:

M → A = a P 1 - 2 3 3 j → - a P 1 + 2 3 - 3 3 i →  

M → A = - a P 9 - 2 3 3 i →   +   a P 3 - 2 3 3 j →

Passo 4

d) Agora precisamos verificar se o sistema é redutível a uma única força.

Uma forma de fazermos isso é calculando o invariante escalar I , lembrando que podemos tomar o momento em relação a qualquer polo.

I = M → D ⋅ R → =     - a P i → + a P j → ⋅ - 3 3 P i → + 3 - 3 3 P j → + 3 - 3 3 P k →

I = 3 a P 2 3 + 3 - 3 3 a P 2 ≠ 0

Perfeito! Como o invariante escalar é diferente de zero, temos que o sistema não é redutível a uma única força.

Valeu gente, terminamos mais uma! Espero vocês na próxima questão! 😉

Resposta

a) R D → =   - 3 3 P i → + 3 - 3 3 P j → + 3 - 3 3 P k →    

M → D = a i → + a j → - a k → × - P k → =   - a P i → + a P j →

b) 0

c) M → A = - a P 9 - 2 3 3 i →   +   a P 3 - 2 3 3 j →

d) Resolução no texto.

Exercícios de Livros Relacionados

Exercício de Livro
O comprimento não deformado da mola A B é 3m . Se o bloco é mantido na posição de equilíbrio mostrada, determine a massa do bloco em D .
O suporte deslizante é usado para apoiar partes de chapas longas enquanto elas são cortadas por uma serra de bancada. Se a chapa exerce uma força direcionada para baixo de 25N no rolete C , determine
O guincho é usado para suspender o motor de 200k g . Determine a força que atua no cilindro hidráulico A B , as componentes horiozntal e vertical da força no pino C e as reações no apoio fixo D .
Todos as soluções dos problemas precisam incluir um diagrama de corpo livre.F5.3. A treliça é suportada por um pino em A e um rolete em B. Determine as reações dos apoios.